Czworokąt wpisany w okrąg.
Zdzisław:
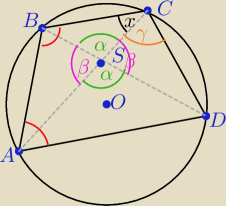
Przekątne AC i BD czworokąta ABCD, wpisanego w okrąg o środku O, przecinają się w punkcie S.
Oblicz miarę kąta
|∡ACD|, jeśli masz dane: |∡DAB|=80
o, |∡BSC|=50
o, |∡ABC|=110
o.
1.Więc tak:
Jest to czworokąt wpisany w okrąg, więc sumy miar przeciwległych kątów czworokąta są równe.
Ma to miejsce tylko wtedy, gdy suma dwóch przeciwległych kątów czworokąta jest równa 180
o.
2.Więc:
|∡DAB| +
|∡ACD| + |∡ACB| = 180
o
80
o +
|∡ACD| + |∡ACB| = 180
o
|∡ACD| + |∡ACB| = 100
o ⇒
|∡ACD| = 100
o −
|∡ACB|
3.Kwestia wyliczenia |∡ACB|:
Możemy skorzystać z trójkąta
ΔABC
180
o=|∡ABC| +
|∡ACB| +
|∡CAB|
180
o=110
o +
|∡ACB| +
|∡CAB|
70
o=
|∡ACB| +
|∡CAB| ⇒
|∡ACB| = 70
o −
|∡CAB|
|∡ACD| = 100
o − 70
o +
|∡CAB| = 30
o +
|∡CAB|
4.Teraz trzeba obliczyć kąt
|∡CAB|:
Można go uzyskać z trójkąta
ΔASB, ponieważ
|∡CAB|=
|∡SAB|
Wiemy że kąt
β =
|∡ASB| = 130
o
180
o=
|∡SAB| + |∡ABS| + |∡BSA| ⇔ 180
o =
|∡CAB| + |∡ABS| + |∡BSA|
180
o=
|∡SAB| + |∡ABS| + 130
o
50
o=
|∡SAB| +
|∡ABS| ⇒
|∡ABS| = 50
o −
|∡SAB|
i tak drążę i drążę... da się to łatwiej zrobić?

 Przekątne AC i BD czworokąta ABCD, wpisanego w okrąg o środku O, przecinają się w punkcie S.
Oblicz miarę kąta |∡ACD|, jeśli masz dane: |∡DAB|=80o, |∡BSC|=50o, |∡ABC|=110o.
1.Więc tak:
Jest to czworokąt wpisany w okrąg, więc sumy miar przeciwległych kątów czworokąta są równe.
Ma to miejsce tylko wtedy, gdy suma dwóch przeciwległych kątów czworokąta jest równa 180o.
2.Więc:
|∡DAB| + |∡ACD| + |∡ACB| = 180o
80o + |∡ACD| + |∡ACB| = 180o
|∡ACD| + |∡ACB| = 100o ⇒ |∡ACD| = 100o − |∡ACB|
3.Kwestia wyliczenia |∡ACB|:
Możemy skorzystać z trójkąta ΔABC
180o=|∡ABC| + |∡ACB| + |∡CAB|
180o=110o + |∡ACB| + |∡CAB|
70o=|∡ACB| + |∡CAB| ⇒ |∡ACB| = 70o − |∡CAB|
|∡ACD| = 100o − 70o + |∡CAB| = 30o + |∡CAB|
4.Teraz trzeba obliczyć kąt |∡CAB|:
Można go uzyskać z trójkąta ΔASB, ponieważ |∡CAB|=|∡SAB|
Wiemy że kąt β = |∡ASB| = 130o
180o=|∡SAB| + |∡ABS| + |∡BSA| ⇔ 180o = |∡CAB| + |∡ABS| + |∡BSA|
180o=|∡SAB| + |∡ABS| + 130o
50o=|∡SAB| + |∡ABS| ⇒ |∡ABS| = 50o − |∡SAB|
i tak drążę i drążę... da się to łatwiej zrobić?
Przekątne AC i BD czworokąta ABCD, wpisanego w okrąg o środku O, przecinają się w punkcie S.
Oblicz miarę kąta |∡ACD|, jeśli masz dane: |∡DAB|=80o, |∡BSC|=50o, |∡ABC|=110o.
1.Więc tak:
Jest to czworokąt wpisany w okrąg, więc sumy miar przeciwległych kątów czworokąta są równe.
Ma to miejsce tylko wtedy, gdy suma dwóch przeciwległych kątów czworokąta jest równa 180o.
2.Więc:
|∡DAB| + |∡ACD| + |∡ACB| = 180o
80o + |∡ACD| + |∡ACB| = 180o
|∡ACD| + |∡ACB| = 100o ⇒ |∡ACD| = 100o − |∡ACB|
3.Kwestia wyliczenia |∡ACB|:
Możemy skorzystać z trójkąta ΔABC
180o=|∡ABC| + |∡ACB| + |∡CAB|
180o=110o + |∡ACB| + |∡CAB|
70o=|∡ACB| + |∡CAB| ⇒ |∡ACB| = 70o − |∡CAB|
|∡ACD| = 100o − 70o + |∡CAB| = 30o + |∡CAB|
4.Teraz trzeba obliczyć kąt |∡CAB|:
Można go uzyskać z trójkąta ΔASB, ponieważ |∡CAB|=|∡SAB|
Wiemy że kąt β = |∡ASB| = 130o
180o=|∡SAB| + |∡ABS| + |∡BSA| ⇔ 180o = |∡CAB| + |∡ABS| + |∡BSA|
180o=|∡SAB| + |∡ABS| + 130o
50o=|∡SAB| + |∡ABS| ⇒ |∡ABS| = 50o − |∡SAB|
i tak drążę i drążę... da się to łatwiej zrobić? 
 t+x=80o
z+t=110o
y+x=70o
z+y=100o
4 niewiadome, 4 równania
dodatkowo
y+t=130o
x+z=50o
z+y+y+x=170o
50o+2y=170o
y=60o
co szukaliśmy
t+x=80o
z+t=110o
y+x=70o
z+y=100o
4 niewiadome, 4 równania
dodatkowo
y+t=130o
x+z=50o
z+y+y+x=170o
50o+2y=170o
y=60o
co szukaliśmy
