Równanie trygonometryczne MR2014 Michoś: Zadanie z Matury Rozszerzonej 2014 Rozwiąż równanie √3cosx = 1+sinx w przedziale <0; 2π>. Byłby w stanie ktoś mi wyjaśnić dlaczego przy obustronnym podniesieniu do kwadratu powstaje na końcu dodatkowe rozwiązanie (5/6π)? to jest : √3cosx = 1+sinx √3cos²x = (1+sinx)² 3 − 3sin²x = 1 + 2sinx + sin² dalej powstaje równanie kwadratowe 2sin²x + sinx − 1 = 0 i dostaje wyniki : sinx = −1 v sinx = 1/2 x = −π/2 +2kπ v x = π/6 +2kπ v x = 5/6π +2kπ Na końcu w podanym przedziale dostaję wyniki x∊{π/6 , 5/6π, 3/2π} a tego 5/6π być nie powinno.. Dziękuję pięknie za odpowiedź

Adamm: ponieważ działanie podnoszenia do kwadratu nie jest przejściem równoważnym jeśli x=−1 to x²=1 ale jeśli x²=1 to x=1 lub x=−1

Michoś: ciężkie to, nie mogę tego rozkminić.. a + b = c + d (a+b)² = (c+d)² o to chodzi, że w tym przypadku miałbym tak jakby osiem wyników ?

Adamm: o to chodzi że jeśli 2=2 to 2²=2² ale już 2=−2 nie zachodzi

Michoś: kiedy więc obustronne podnoszenie do kwadratu ma sens ? tak jest w przypadku mnożenia ?

Adamm: jeśli masz a=−a to podnosząc do kwadratu obustronnie dostaniesz a²=a² czyli prawdę chodzi właśnie o to że podnosząc do kwadratu nie wiesz jakich znaków są obie strony do kwadratu można podnosić tylko wtedy kiedy obie strony są dodatnie, w przeciwnym razie mogą dojść złe wyniki

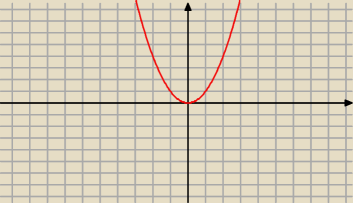
Adamm: spójrz tylko na parabolę każdej wartości x² odpowiada zarówno −x jak i x

Adamm: czyli na przykład jeśli mamy x²=a i np. weżniemy obie strony pod funkcję sinx to mamy sin(x²)=sina tutaj wyjdzie nieskończenie wiele możliwych wartości x, w odróżnieniu od co najwyżej dwóch tak jak na początku

Michoś: kurczę, wydaje mi się, że zacząłem łapać przeraża mnie fakt, że chyba mam jakiegoś przedmaturalnego laga mózgu i cofnąłem się do 1 klasy D: zapytam jeszcze, jeżeli hipotetycznie mam nierówność ab = c to nie ma problemu jeżeli zrobię z tego (ab)² = c² ?

Adamm: jaką nierówność? napisałem: spójrz tylko na parabolę, każdej wartości x² odpowiada zarówno −x jak i x

Michoś: tak, tak równania kwadratowe i wszystko ogarniam tylko problem mam cały czas z tym podnoszeniem obustronnym... masakra, coś mnie to przerasta OKEY, chyba rozumiem! To jest poziom liceum ? Wydaje mi się, że coś przeoczyłem hah Dziękuję pięknie!

Adamm: poziom liceum? zwykłe logiczne myślenie

zef: Te równanie można rozwiązać za pomocą podniesienia obustronnie do kwadratu, ale na koniec mając rozwiązania trzeba je podstawić i sprawdzić czy równanie jest prawdziwe. Wynika to z tego że mogą pojawić się tzw. pierwiastki obce (Eta mi to kiedyś już tłumaczyła ). Te równanie jednak lepiej podzielić przez 2 i sprowadzić do wzorów redukcyjnych, wtedy nie musimy sprawdzać tych pierwiastków.

Mila: √3cosx = 1+sinx w przedziale <0; 2π> √3cosx−sinx=1 /:2

	1		1
U{p3}}{2}*cosx−		sinx=		⇔
	2		2

	π		π		1
sin		*cosx−sinx*cos		=
	3		3		2

	π		1
sin(		−x)=
	3		2

	π		1
sin(x−		)=−
	3		2

	π		7π		π		11π
x−		=		+2kπ lub x−		=		+2kπ i x∊<0; 2π>
	3		6		3		6

	3π		13π
x=		+2kπ lub x=		+2kπ
	2		6

	3π
k=0 to x=
	2

	π
k=−1 to x=
	6

==============

Mateusz: Zagadnienie stare jak świat przykładowo: √x+4 = x−2 założenie że x+4≥0 podnosze do kwadratu: (√x+4)² = (x−2)² x+4=x²−4x+4 x(x−5)=0 x=0 v x=5 i co się stało 0 nie spełnia równania wyjściowego a dzieje się to dlatego że podnoszenie do kwadratu obu stron równania nie zawsze daje równania równoważne w odróżnieniu np od mnożenia obu stron równania przez liczbę różną od zera Jak wytropić zatem taki obxcy pierwiastek tak jak ktoś napisał podstawić rozwiązanie do równania i sprawdzić