 Ratujemy .... "tonącego"
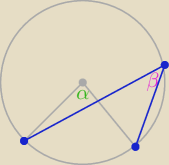
Ratujemy .... "tonącego"  1/ 2β=α i α+β=147o to 3β=147o ⇒ β=49o i α=98o
1/ 2β=α i α+β=147o to 3β=147o ⇒ β=49o i α=98o
| 1 | 1 | |||
2/ P= | c*h ⇒ 3c=27 ⇒ c=9 to R= | c=4,5 | ||
| 2 | 2 |
| fe | ||
f2+e2=4a2 ⇒ (f+e)2−2fe=4*64 ⇒ 400−2fe=4*64 /: 4 ⇒ | =P=36 | |
| 2 |
| P | 36 | |||
h= | = | =4,5 | ||
| a | 8 |
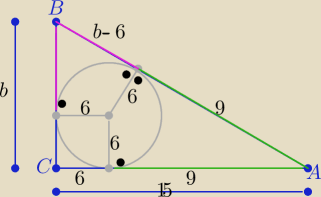
| 15*b | ||
4/ P(ABC)= | i P(ABC)=(b−6)*9 | |
| 2 |
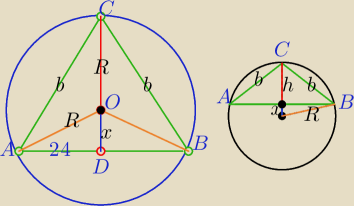 3) I przypadek:
R=26
Srednica d=2R=52
|AB|=48
W ΔADO:
R2=x2+|AD|2⇔262=x2+242⇔x2=100
x=10
|CD|=26+10=36
W ΔADC:
b2=242+362=576+1296=1872
b=√1872=√144*13=12√13
b=12√13
=========
II przypadek
X2+242=262
x=10
h=26−10=16
b2=242+162
b2=576+256=832
b=√832=√64*13
b=8√13
=======
3) I przypadek:
R=26
Srednica d=2R=52
|AB|=48
W ΔADO:
R2=x2+|AD|2⇔262=x2+242⇔x2=100
x=10
|CD|=26+10=36
W ΔADC:
b2=242+362=576+1296=1872
b=√1872=√144*13=12√13
b=12√13
=========
II przypadek
X2+242=262
x=10
h=26−10=16
b2=242+162
b2=576+256=832
b=√832=√64*13
b=8√13
=======


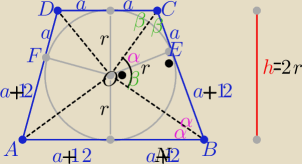 Na rysunku oznaczyłam dane z twierdzenia o odcinkach stycznych
oraz h=2r =16
i w prostokątnym ΔCOB (bo kąt BOC =90o
r2=a(a+12) ⇒ a2+12a−64 =0 ⇒(a−4)(a+16)=0 ⇒ a=4
Obwód trapezu L= 8a+48=...=80
Na rysunku oznaczyłam dane z twierdzenia o odcinkach stycznych
oraz h=2r =16
i w prostokątnym ΔCOB (bo kąt BOC =90o
r2=a(a+12) ⇒ a2+12a−64 =0 ⇒(a−4)(a+16)=0 ⇒ a=4
Obwód trapezu L= 8a+48=...=80
| 4a+24 | ||
Pole trapezu : P= | *h= ......=320 | |
| 2 |