Sześcian przecięto płaszczyzną przechodzącą przez krawędź podstawy
idiota :(: Sześcian przecięto płaszczyzną przechodzącą przez krawędź podstawy i nachyloną do płaszczyzny
podstawy pod kątem α < 45. Pole powierzchni całkowitej mniejszej z otrzymanych brył, jest
równe połowie pola powierzchni całkowitej sześcianu. Oblicz tg α.
11 kwi 20:47
piotr: 2tgα + 1/cosα = 2
11 kwi 20:57
Pomocy: O.o Mógłbyś wyjaśnić skąd i dlaczego bym mógł zrozumieć na przyszłość?
11 kwi 20:59
piotr:
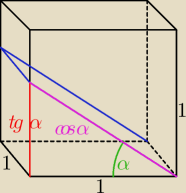
11 kwi 21:10
piotr: Psz = 6
P< = 1*tgα + 2*tgα/2 +1/cosα + 1 = 3
11 kwi 21:11
Mila:
Masz może odpowiedź do zadania?
11 kwi 22:43
pomocy: No właśnie niestety nie posiadam. Profesor dał nam ksero zadania, którego nie mamy w książce

12 kwi 00:04
pomocy: Nawet spoglądając na to co uczynił użytkownik piotr to nadal nie wiem "jak to ugryźć" bym mógł
samemu to doprowadzić do takiejże postaci
12 kwi 00:05
Mila:
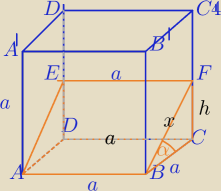
α<45
o⇔h=| FC|<a i tgα<1
| | a | | h | |
W ΔBCF: cosα= |
| , tgα= |
| |
| | x | | a | |
P
csz=6a
2
| | 1 | |
Pcg= a2+a*x+a*h+2* |
| a*h −−pow. graniastosłupa |
| | 2 | |
P
cg=a
2+ax+2*a*h
Z treści zadania:
a
2+ax+2*a*h=3a
2⇔
ax+2ah=2a
2 /:a
2
√1+tg2α+2tgα=2 , tgα=t,t∊(0,1)
√1+t2=2−2t obie strony dodatnie 2−2t>0⇔
1+t
2=4−8t+4t
2
po rozwiązaniu:
| | 4−√7 | | 4+√7 | | 4+√7 | |
tgα= |
| lub tgα= |
| ∉D bo |
| >1 |
| | 3 | | 3 | | 3 | |
posprawdzaj rachunki.
12 kwi 00:26


 α<45o⇔h=| FC|<a i tgα<1
α<45o⇔h=| FC|<a i tgα<1