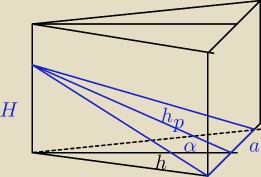
Przekrój graniastosłupa prawidłowego trójkatnego, zawierający krawędź dolnej podstawy i punkt
przeciwległej krawędzi bocznej, jest nachylony do płaszczyzny podstawy pod kątem α = 30stopni.
Oblicz pole tego przekroju, jeśli wiadomo, że odcina on od danego graniastosłupa ostrósłup o
objętości V
| 2√6 | ||
= | ||
| 3 |
| H | a√3 | |||
tg30 = | , h= | |||
| h | 2 |
| a | ||
po przeksztalceniach H = | ||
| 2 |
| 2√6 | 1 | a2√3 | ||||
V = | = | * | * H | |||
| 3 | 3 | 4 |
| a | ||
Podstawiam pod H | i dostaję jakiś kosmos, a ma się równać 2√2 = a | |
| 2 |
