f. kwadratowa - dziedzina Delcik: Dla jakiego parametru m, dziedziną funkcji f(x)= √(m²−m)x²−2mx+1 jest zbiór liczb rzeczywistych?

Delcik: Tzn wiem, że to co pod pierwiastkiem musi być większe bądź równe zero. Ale i tak nie wiem co mam z tym zrobić.

Jerzy: 1) m² − m > 0 2)Δ ≥ 0

zef: zał.: (m²−m)x²−2mx+1≥0 ⇔ Δ≤0, m²−m>0 Oraz sprawdź co się dzieje dla a=0

Jerzy: Poprawka: 2) Δ ≤ 0

Delcik: 1. @zef zmienia się w f. liniową i co z tego? 2. (m2−m)x2−2mx+1≥0 to wiem i rozumiem. Ale to delta w końcu Δ≤0 czy Δ ≥ 0? i czemu?

Delcik: No to czemu Δ ≤ 0?

zef: A o czym informuje nas delta w równaniach kwadratowych ?

Delcik: O miejscu zerowym. Jeżeli większa od zera to dwa rozwiązania. jeżeli równa 0 to jedno. Jeżeli mniejsza to nie ma miejsc zerowych

Delcik: Ale nadal nie umiem z tego wyciągnąć wniosków

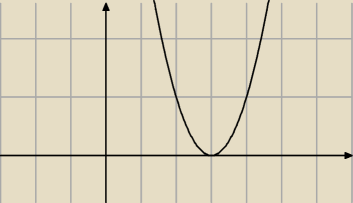
zef: No właśnie a chcesz żeby całość pod pierwiastkiem była większa lub równa zero. Żeby tak było to wyrażenie pod pierwiastkiem musi mieć ramiona skierowane ku górze (a>0) oraz nie mieć miejsc zerowych lub mieć jedno

Delcik: To ma sens m=0 v m=1 m należy do (−oo;0) U (1;+oo) z delty wychodzi m≤ 0 czyli m nalezy do (−oo;0>?

Delcik: tzn dziedzina to m nalezące do (−oo;0>?

zef: Niech ktoś inny już obliczenia sprawdzi, ważne że już to rozumiesz

Delcik: Dziękuję!