rys przyszłymakler: mam małe zaćmienie:

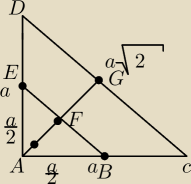
	a√2
Wszystko tak jak na rysunku, tj. AE= AB = a/2 AG=
	2

	a√2
Jak udowodnić, że GF =		to wydaje się tak oczywiste, że aż nie wiem jak to
	4

udowodnić.

Metis: Ja dopatrywałbym się jakiś podobieństw, ale z geometrii to jestem noga

przyszłymakler: Ja widzę, że EGBA tworzą kwadrat i to musi być połowa przekątnej kwadratu o długości a/2, ale chciałbym inaczej to udowodnić.

Eta:

	a√2		a√2
|GF|= |AG|−|AF|= a√2−		=
	2		2

Popraw treść zadania

Adamm: Eta, głupoty piszesz

Eta: Co?

Adamm: no bo... |AG|≠a√2... no i... |AF|≠a√2/2...

Eta: Źle odczytałam treść ( sorry

Eta:

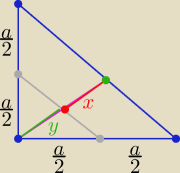
	√2
Nie zauważyłam ,że napisałeś |AG|=
	2

Z podobieństwa trójkątów w skali k=2

	1		√2		√2
y=|AF|=		|AG| =		a ⇒ x=|AF|=|AG|−|AF|=.......=		a
	2		4		4