całki Metis: Kilka całek Może mi ktoś pokazać jak poprawnie( chodzi głównie o zapis) rozwiązać te całki: Całkę podwójną ∫∫_D f(x,y)dxdy zamienić na całki iterowane, jeżeli obszar D ograniczony jest krzywymi o równaniach: Zacznijmy od prostego: y = x², y = x + 2; x² + y² = 4, y = 2x − x², x = 0 (x, y ­≥ 0) x² − y² = 1, x² + y² = 3 (x < 0).

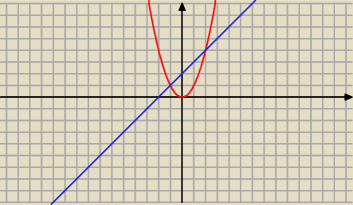
Adamm: najpierw narysuj sobie obszar wyznaczasz punkty przecięcia, x+2=x2 ⇒ x=−1 lub x=2 zbiór D przedstawiasz tak D={(x; y): x2≤y≤x+2, −1≤x≤2} teraz piszesz tak ∫∫Df(x; y)dxdy=∫−12∫x2x+2f(x; y)dydx nie jestem pewien czy można zawsze tak zamieniać, mam na myśli dy z dx, ale w większości przypadków można co najwyżej można zmienić obszar

zef: Przecież pierwszy obszar można wyznaczyć za pomocą całki pojedynczej

Metis: zef wiem. Mam to rozwiązane, ale zaniedbałem zapis matematyczny i nie chce stracić pkt. na kolokwium.

Benny: Nie zawsze da się tak zmienić. Jak dobrze kojarzę to tw. Fubiniego.

Benny: Chociaż tutaj nie całkujemy po iloczynie kartezjańskim, więc nie powinno być problemów.

Metis: Nie zgadza mi się coś 2) Może ktoś zerknąć? Jaki będzie obszar całkowania?

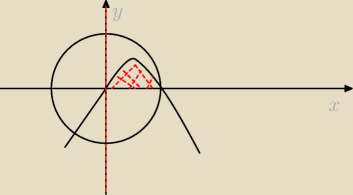
Metis: 0≤x≤2 a po y?

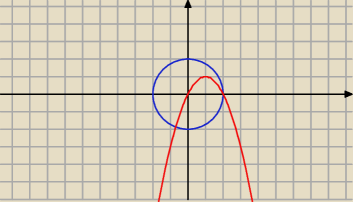
Adamm: są dwa możliwe obszary 0≤x≤2 dla obu pierwszy do 0≤y≤x², a drugi to x²≤y≤√4−x² nie podają dokładnie który