Mamy ostrosłup trójkątny prawidłowy o boku podstawy 3 cm, jego wysokość znajduje AveHidan: Witam, dzisiaj na egzaminie dostałem piękne zadania których nie wiem wgl z której strony zajść. Podam przykład z pamięci: Mamy ostrosłup trójkątny prawidłowy o boku podstawy 3 cm, jego wysokość znajduje się na jednym z wierzchołków, a nachylenie ściany bocznej która nie zawiera wierzchołka z wysokością ostrosłupa jest nachylona do podstawy pod kątem 45 stopni. Oblicz wszystko, tj. wysokość, objętość, pole całkowite i długość krawędzi. Domyślam się że kluczowe jest użycie funkcji trygonometrycznych, ale nawet kiedy zerknąłem na wzory funkcji, w dalszym ciągu nie wiem jak ich użyć żeby mi pomogły. Będę bardzo wdzięczny za czytelne rozpisanie zadania krok po kroku (zwłaszcza na początku przy używaniu funkcji trygonometrycznych, może być też ze słownym dopiskiem), bo kiedy mam już jakieś 2 wartości czyli podaną długość ściany bocznej i podstawy etc. to wyliczenie objętości, pp i pc nie jest dla mnie problemem, problemem jest wyliczenie tej niezbędnej drugiej wartości. Wielkie dzięki z góry za pomoc

Mila: Jeżeli prawidłowy trójkątny to spodek wysokości nie może być znajdować się w wierzchołku podstawy. Musisz napisać dokładną treść.

AveHidan: Zadzwoniłem do koleżanki z klasy żeby skonsultować treść zadania (nie jest możliwe przepisanie oryginału) i treść brzmi tak jak napisałem co do joty. Potwierdziła ona też informację że spodek wysokości nie może być w wierzchołku podstawy, więc samo zadanie było kpina na dobrą sprawę. Warto wziąć pod uwagę że pisała je nauczycielka własnoręcznie W takim razie, jeśli mogę prosić, pomiń tą część z wierzchołkiem i przyjmij że znajduje się tam gdzie ma się znajdować, chodzi o sposób użycia funkcji trygonometrycznych w tego rodzaju zadaniach, jutro mam ustny z matmy i będę miał tego samego typu zadania, więc muszę to zrozumieć

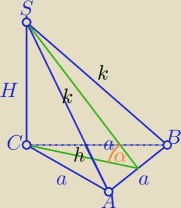
Mila: Może o to chodziło? a=3 α=45^o

Mila: Takie zadania z wysokością w wierzchołku są bardzo często. Nie jest to jednak ostrosłup prawidłowy trójkątny. To rozwiążcie wg mojego rysunku, po kolacji narysuję ostrosłup prawidłowy trójkątny.

AveHidan: h² + 1/2² = 3² h= √6,75 Nie wiem jak wyliczyć k lub H funkcją trygonometryczną, wzory na nie mam, ale nic mi nie mówią, do tego doszedłem na samym sprawdzianie Jak dowiem się jak to obliczyć (bo tego wlaśnie potrzebuję wiedzieć ) to z resztą nie będzie raczej problemu

AveHidan: PS. może nie był prawidłowy, ale o podstawie trójkąta równobocznego, to pewne

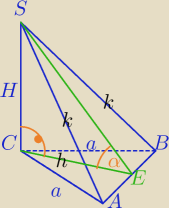
Mila: ΔABC− Δrównoboczny o boku a=3 1)

	a√3		3√3
h=		=
	2		2

	a2√3		32√3		9√3
PΔ=		=		=
	4		4		4

2) Ty obliczyłeś h z tw. Pitagorasa ( dobrze)

	3		27
6		=
	4		4

	√27		√9*3		3√3
h=		=		=		to samo, ale więcej liczenia.
	√4		2		2

3) jeżeli α=45^o to oznacza, że ΔSCE ) jest trójkątem prostokątnym równoramiennym.

	3√3
H=h=
	2

4)

	1		32√3		3√3		27
V=		*		*		=
	3		4		2		8

============================== 5)

	9√3		1
Pc=		+2*		*a*H+PΔABS
	4		2

	3√3		3√6
|SE|=h√2=		*√2=		(wzór na przekątna kwadratu d=a√2)
	2		2

albo tak:

	H
sin45o=
	|SE|

√2		3√3   2		3√3
	=		⇔√2*|SE|=2*
2		|SE|		2

√2*|SE|=3√3 /*√2 2*|SE|=3√6

	3√6
|SE|=
	2

	9√3		1		3√3		1		3√6
Pc=		+2*		*3*		+		*3*
	4		2		2		2		2

============================ dokończ rachunki 7) k²=a²+H²

AveHidan: Ahh no tak... to trójkąt równoramienny... sam nie wierzę w wielkość swojej głupoty czasem, nigdy bym na to nie wpadł I nagle wszystko nabiera sensu... A wytłumaczysz mi jak obliczyłaś bok ISEI za pomocą sinusa bo nie rozumiem nic z tego co napisałaś? (rzecz jasna jeśli chodzi o sinusa)

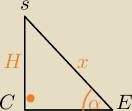
Mila: z definicji:

	H
sinα=
	x

Z treści:

	H		√2
sin45=		( sin 45=		jest w tablicach, ale powinno być już w Twojej główce)
	x		2

√2		H
	=		mnożę na krzyż ( nie postawiam jeszcze wartości,
2		x

bo widzę, że masz kłopoty z rachunkami)

Mila: Dalej, wysłało się nieopatrznie: x*√2=2*H

	3√3
x*√2=2*
	2

x*√2=3√3 /*√2 x*2=3√3*2 2x=3√6 /:2

	3√6
x=
	2

===========

AveHidan: Ahh rozumiem, czyli wystarczy że wzór sin a = a/c pomnożę na krzyż przez to co wychodzi z tablic wartości trygonometrycznych i wtedy wychodzi mi długość boku SE? Znaczy nie widzę innej możliwości, ale wolałbym dostać jeszcze proste potwierdzenie, nota bene to jest właśnie rzecz której nie wiedziałem, co z jednym i drugim się robi, a skoro dobrze to rozumiem to chyba problem z głowy Czekam na potwierdzenie, ale mimo wszystko już teraz bardzo Ci dziękuje za poświęcony czas, w życiu nie znalazł bym odpowiedzi na to pytanie w internecie gdybym po prostu szukał

Mila: Zaraz, bo coś tłumaczę pewnej miłej panience.

Mila:

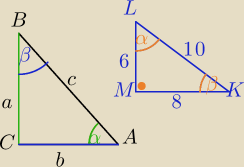
	a
sinα=		( przyprostokątna leżąca naprzeciw kąta do przeciwprostokątnej)
	c

	b
sinβ=
	c

To oblicz sinusy kątów ostrych w trójkącie KLM.

AveHidan: sin a= 6/10=3/5 sin B= 8/10=4/5 O to chodziło?

Mila: No nie! Mianowniki dobre. Co leży naprzeciw kąta α ?

AveHidan: aha! czyli odwrotnie czyli sin a=4/5 sin B =3/5

Mila: Teraz dobrze.

AveHidan: Dzięki wielkie za pomoc!

Mila: Powodzenia jutro

AveHidan: Przyda się, ale myślę że dzięki Tobie to 2 na święty spokój jest bliżej niż dalej, jeszcze raz dzięki