Rozważmy eksperyment związany z grą w darta asd: Rozważmy eksperyment związany z grą w darta: rzucamy lotką do tarczy w kształcie koła o promieniu jednostkowym. Niech X – zmienna losowa reprezentująca odległość punktu, w którym wyląduje lotka, od środka tarczy. Zakładając, że lotka zawsze wyląduje na tarczy i że każdy punkt tarczy ma identyczną szansę na trafienie, odpowiedzieć na pytania: (a) Jaki jest zbiór wartości X? (b) Znaleźć P(X < a) oraz P(a < X < b), gdzie: a < b ≤ 1. Czy ktoś mógłby chociaż pomóc naprowadzić na rozwiązanie tego zadania ?

g: 0 ≤ X ≤ 1 P(X<a) = πa² / π1² = a² P(a<X<b) = b² − a²

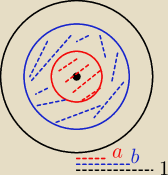
Pytający: a) <0,1> // przy trafieniu w środek tarczy wartość to 0, przy trafieniu w brzeg wartość to 1 (promień) b) Prawdopodobieństwo geometryczne: P(X < a) − prawdopodobieństwo trafienia w koło o tym samym środku co tarcza i promieniu a

	πa2
P(X < a)=		=a2
	π12

P(X < a) − prawdopodobieństwo trafienia w obszar ograniczony okręgami o tym samym środku co tarcza i promieniach a, b

	πb2−πa2
P(a < X < b)=		=b2−a2
	π12