Punkty A, B, C leżą na sferze o promieniu R w taki sposób że |AB|=|BC|=2|AC|=R.
Jasiek2234:
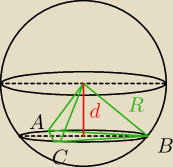
Punkty A, B, C leżą na sferze o promieniu R w taki sposób że |AB|=|BC|=2|AC|=R.
Wyznacz odległość środka sfery od płaszczyzny ABC.
Czyli mam ostrosłup o podstawie ABC wpisanej okrąg(przyjmijmy promień r) i wierzchołku w środku
sfery.
Krawędzie boczne są równej długości, więc spodek wysokości to środek tego okręgu.
z tw. Pitagorasa
d
2 =
√R2 − r2
czyli szukam promienia okręgu opisanego na podstawie
z tw.sinusów
|AC|
2/sinα = 2r α=|∡ABC|
|AC| = R/2
r = R/4sinα
sin
α2 = 1/4
sinα = 2sin
α2cos
α2 = 2*
14*
√1516 =
√158
r = 2R/
√15
d = R
√1115
Według odpowiedzi powinno być d = R
√16515 gdzie robię błąd
10 kwi 11:41
jc:
11*15 = 165, dlatego √11/15 = √165 /15. To samo, tylko nieskrócone.
10 kwi 11:52
g: Tw. sinusów to |AC| / sinα = 2r, ale dalej jest dobrze. Nie widzę błędu.
10 kwi 12:06
Jasiek2234: Faktycznie to samo :'D. Przy |AC| źle przepisałem, w obliczeniach tego kwadratu nie mam. Dzięki

10 kwi 13:42
 Punkty A, B, C leżą na sferze o promieniu R w taki sposób że |AB|=|BC|=2|AC|=R.
Wyznacz odległość środka sfery od płaszczyzny ABC.
Czyli mam ostrosłup o podstawie ABC wpisanej okrąg(przyjmijmy promień r) i wierzchołku w środku
sfery.
Krawędzie boczne są równej długości, więc spodek wysokości to środek tego okręgu.
z tw. Pitagorasa
d2 = √R2 − r2
czyli szukam promienia okręgu opisanego na podstawie
z tw.sinusów
|AC|2/sinα = 2r α=|∡ABC|
|AC| = R/2
r = R/4sinα
sinα2 = 1/4
sinα = 2sinα2cosα2 = 2*14*√1516 = √158
r = 2R/√15
d = R√1115
Według odpowiedzi powinno być d = R√16515 gdzie robię błąd
Punkty A, B, C leżą na sferze o promieniu R w taki sposób że |AB|=|BC|=2|AC|=R.
Wyznacz odległość środka sfery od płaszczyzny ABC.
Czyli mam ostrosłup o podstawie ABC wpisanej okrąg(przyjmijmy promień r) i wierzchołku w środku
sfery.
Krawędzie boczne są równej długości, więc spodek wysokości to środek tego okręgu.
z tw. Pitagorasa
d2 = √R2 − r2
czyli szukam promienia okręgu opisanego na podstawie
z tw.sinusów
|AC|2/sinα = 2r α=|∡ABC|
|AC| = R/2
r = R/4sinα
sinα2 = 1/4
sinα = 2sinα2cosα2 = 2*14*√1516 = √158
r = 2R/√15
d = R√1115
Według odpowiedzi powinno być d = R√16515 gdzie robię błąd
