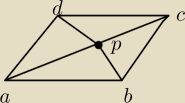
dowód Cpt. Dżak Sparoł: Ahoj , w równoległoboku abcd punkt P leży na przekątnej AC.Wykaż że pola ΔABP i APD są podobne I teraz moje próba dowodu brzmi następująco − Trójkąty te są podobne − z cechy np.kbk. Odległość punku P od wierzchołków D i B zawsze będzie tak sama niezależnie od położenia punktu P na przekątnej. Wysokosći tych trójkatów będe równiez takie same tak samo jak ich podstawy co daje nam pole takie same . CKD Czy takie coś by przeszło ?

Adamm: pola trójkątów są podobne?

Cpt. Dżak Sparoł: Oj znaczy równe , przepraszam mój błąd

Adamm: to jest romb czy równoległobok, bo piszesz jakby był rombem

Cpt. Dżak Sparoł: Równoległobok

Adamm: no dobra, wytłumacz o który bok oraz które kąty ci chodzi gdy mówisz z cechy kbk są podobne

Adamm: od razu mówię: kąt BAP nie jest równy kątowi PAD

Cpt. Dżak Sparoł: W zasadzie to cała moje teoria legła w gruzach gdyż założyłem sobie ze przekątna ac przetnie kat przy wierz. A na pół , a niestety nie przetnie.

Adamm: oba trójkąty mają wspólną podstawę |AP| ΔABC∼ΔACD wysokości trójkątów ABC, ACD mają wysokość tej samej długości, padającą na bok AP a te trójkąty mają taką samą wysokość jak ΔADP oraz ΔABP mają takie same podstawy i wysokości, czyli takie same pola

Cpt. Dżak Sparoł: Dziękuję