prawdopodobiensto wojtek: z urny w ktorej jest 7 kul bialych i 6 czarnych usunieto w sposob losowy jedna kkule a nastepnie wylosowano dwie kule ktore ze zzdarzen jest bardziej prawdopodobne A − wylosowanie dwoch kul czarnych pod warunkiem ze usunieto kule biala B wylosowanie dwoch roznych kul pod warunkiem ze usunieto kule czarna mozecie mi do tego ttez drzewko rozrysowac?

wojtek: ref

wojtek: .

wojtek: help

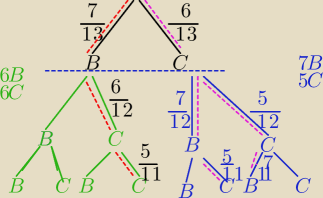
Mila: 7B,6C Licz

wojtek: ale mam to sobie po prostu wymnazac czy to jesy praw. warunkowe? bo zrobilem tak jak ty, a niektorzy mi pisali zeto warunkowe jest

Pytający: Przecież masz w treści napisane "pod warunkiem, że...", czyli tak − jest to prawdopodobieństwo warunkowe. P(A) na logikę: Wiesz, że usunięto kulę białą (taki masz warunek), więc sytuacja bez tej kuli jest Twoim "stanem początkowym" dla którego liczysz prawdopodobieństwo, że wylosujesz 2 czarne kule. Stąd

	6		5
P(A)=		*		// masz po 6 kul i losujesz 2 czarne
	12		11

Jak widać, jest to wymnażanie wg drzewka poniżej zaznaczonej poziomej kreski (oddzielającej oba warunki). P(A) ze wzoru na prawdopodobieństwo warunkowe: C − wylosowanie dwóch kul czarnych D − usunięto kule białą C∩D − usunięto kule białą i wylosowano dwie kule czarne

	P(C∩D)		7   6   5   * * 13   12   11		6		5
P(A)=P(C|D)=		=		=		*
	P(D)		7   13		12		11

P. warunkowe możesz liczyć drzewkiem.