Równanie logarytmiczne z parametrem
Cassandra: Dla jakich wartości m równanie:
logx−2(16−x)=m2−4 ma rozwiązanie ?
9 kwi 22:26
9 kwi 22:28
Cassandra: Hmm, a jak tutaj wyznaczyć zbiór wartości ?
9 kwi 22:31
Adamm: limx→3+ logx−2(16−x) =...
logx→16− logx−2(16−x) = ...
+ funkcja jest ciągła
9 kwi 22:33
Cassandra: Dlaczego tak i jak to policzyc ?
9 kwi 22:53
Adamm: | | log(16−x) | |
limx→3+logx−2(16−x) = limx→3+ |
| =∞ |
| | log(x−2) | |
| | log(16−x) | |
limx→16−logx−2(16−x) = limx→16− |
| =−∞ |
| | log(x−2) | |
ponieważ funkcja jest ciągła to musi przechodzić przez wszystkie wartości z zakresu
ZW=(−
∞;
∞)=ℛ
9 kwi 23:02
Cassandra: Funkcja jest ciągła ? A co z dziedziną ? Przecież x ∉ R
9 kwi 23:09
Adamm: funkcja jest ciągła dla x∊(3;16)
9 kwi 23:11
Cassandra: Nie potrafię sobie tego za bardzo wyobrazić. Może gdybym jakoś narysowała wykres tej funkcji.
9 kwi 23:13
Adamm:
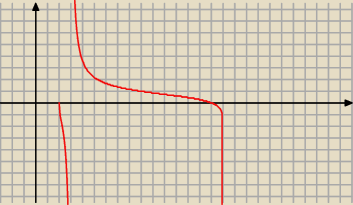
tak to mniej więcej wygląda
9 kwi 23:15
Cassandra: A w jaki sposób to narysować ? Te x−1 trochę mi przeszkadza
9 kwi 23:25
Adamm: trochę trudno byłoby to narysować, lepiej zostawić to maszynie
9 kwi 23:28