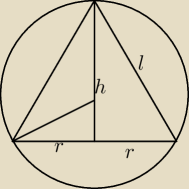
Stereometria Donna: Oblicz wysokość i promień podstawy stożka wpisanego w kulę o promieniu R. R − promień koła r − promień podstawy stożka h − wysokość stożka l − tworząca stożka Napisałam tyle: H² + r² = l²

1		2rll
	rH =
2		4R

... l² = 2RH

g: Wiele różnych stożków można wpisać w kulę. Żeby wybrać jeden, to trzeba jeszcze jakichś danych.

	2rll
Co to jest		?
	4R

Donna: Stożek o największej objętości* Przepraszam, pominęłam.

2rll		abc
	wzór na pole trójkąta
4R		4R

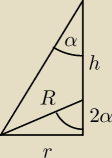g: ok, nie znałem tego wzoru. nie będzie potrzebny, bo nie warto zajmować się bokiem l. sin2α = r/R r = R*sin2α tgα = r/h h = R*sin2α/tgα

	sin32α
Objętość stożka jest proporcjonalna do r2h = R3
	tgα

d(r2h/R3)		6 sin22α cos2α tgα − sin32α/cos2α
	=		= 0
dα		tg2α

po skróceniach sinα=1/√3 itd.

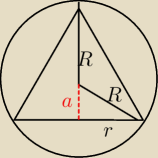Milo: h = a + R a² + r² = R² skąd r² = R² − a² V = 1/3 * πr² * (a+R) = 1/3*π*(R²−a²)(a+R) itd., pochodna po zmiennej a i wiadomo