stereometria

stereometria Krakus: Podstawa stożka o kącie rozwarcia 2α < 90 jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu r

9 kwi 17:29

Adamm: "jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu r" nie rozumiem tego zdania

9 kwi 17:37

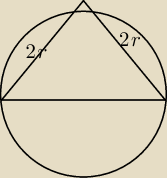
Krakus: rysunek

to chyba o to chodzi

9 kwi 17:42

Krakus: czy ktoś potrafi to rozwiązać?

9 kwi 18:07

Tadeusz: to chyba nie o to "biega" emotka

9 kwi 18:15

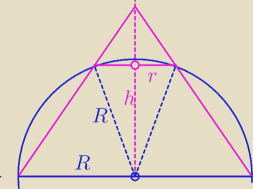
Tadeusz: rysunek

9 kwi 18:27

Tadeusz:

R		r
	=		z tego wyliczysz h i do wzoru na objętość stożka
h		h−√R²−r²

9 kwi 18:31

Krakus: ale przecież jest że jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu r

9 kwi 18:49

Tadeusz: na moim rysunku wycina na Twoim nie bardzo emotka

9 kwi 18:53

Krakus: ale powierzchnia boczna ma wycinać

9 kwi 18:54

Tadeusz: to wczytaj się porządnie. Powierzchnia boczna wycina na powierzchni kuli

9 kwi 18:58

Krakus: a co to jest to h−√R²−r²

9 kwi 19:02

Krakus: który to odcinek bo nie mogę tego zobaczyć

9 kwi 19:03

Adamm: wysokość tego trapezu

9 kwi 19:03

Krakus: ale to nie powinno być √R²−r² bez tego h?

9 kwi 19:05

Adamm: przepraszam, nie wysokość trapezu tylko mniejszego trójkąta

9 kwi 19:08

Krakus: ale √R²−r² jest równe h

9 kwi 19:11

Adamm: nie, h to wysokość większego trójkąta √R²−r² to wysokość trapezu

9 kwi 19:15

Krakus: Dzięki

9 kwi 19:17