Kąt alfa jest ostry Xyz: Kąt α jest ostry i sinα=1/2cosα. Oblicz wartość wyrażenia sinα+cosα.

Jerzy:

	1
tgα =
	2

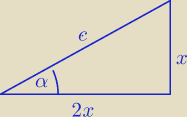
Janek191: sin α = ¹₂ cos α / : cos α

	1
tg α =
	2

c² = x² + 4 x² = 5 x² c = √5 x więc

	x		x		1		√5
sin α =		=		=		=
	c		√5 x		√5		5

	2 x		2		2 √5
cos α =		=		=
	√5 x		√5		5

zatem

	3 √5
sin α + cos α =
	5

'Leszek:

	1
Jezeli to jest podane wyrazenie w postaci sin α =		?
	2 cos α

To : sin α + cos α = x , podnosimy do kwadratu sin² α + 2 sin α * cos α + cos²α = x² ⇒ 2 sin α cos α = x² − 1 i z podanego wyrazenia : 2 sin α cos α = 1 po podstawieniu otrzymasz : x² = 2 ⇒x = √2 Czyli : sin α + cos α = √2

Adamm: sinα+cosα=√2 ⇒ α=π/4