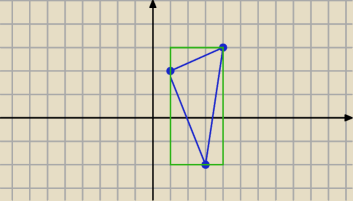
Pole trójkąta ze wzrou Herona hejk: Pole trójkąta o wierzchołkach A(1;2), B(3;−2), C(4;3) ma wartość: A. 14 j² B. 21/2 j² C. 7 j² D. 15/2 j² Obliczyłam długości wszystkich boków i wyszło: |AB| = 2 |BC| = √26 |CA| = √10 Postanowiłam wykorzystać wzór Herona, więc obliczyłam połowę obwodu (p) p = (2+√26+√10)/2 No i potem podstawiłam wszystko pod wzór Herona P = √p(p−|AB|)(p−|BC|)(p−|CA|) Po wymnożeniu wszystkiego wyszło mi: P = √16/16 = √1 = 1 I nie ma takiej odpowiedzi :<

zef: szybciej skorzystać z gotowego wzoru na pole trójkąta znając współrzędne wierzchołków, jeżeli tutaj coś nie wyszło to pewnie błąd w obliczeniach

hejk: omg, rzeczywiście jest taki wzór ;−; Dzięki

Janek191: P_Δ = ( 4 −1)*(3 − (−2)) − 0,5*2*4 − 0,5 *1*5 − 0,5*3*1 = 15 − 4 − 2,5 − 1,5 = 7 j²

Jerzy: Odp: C)

Jerzy: AB^→ = [2;−4] AC^→ = [3;1]

	1
P =		|2 + 12| = 7
	2

Janek191: A = ( 1,2) B = ( 3, − 2) C = (4, 3) II sposób → AB = [ 3 − 1, −2 −2 ] = [ 2, − 4] → AC = [ 4 − 1, 3 − 2] = [ 3, 1] Pole Δ → → P = 0, 5* I det ( AB, AC ) I = 0,5*I 2*1 − 3*(−4) I = 0,5 *I 2 + 12 I = 0,5* 14 = 7 j²