Nierówność z parametrem Piotr: Dana jest nierówność |x−1|+|x+2|<m Wyznacz te wartości parametru m dla których nierówność nie ma rozwiązań.

Piotr: Pomoże ktoś

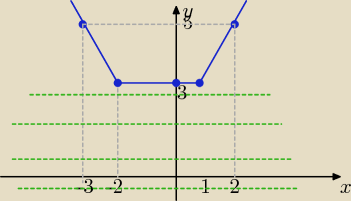
Eta: Zad. można rozwiazać rysując wykres f(x) = Ix −1I + Ix +2I miejsca zerowe pod modułami : x = 1 v x = −2 1)dla x€( −∞, −2) f(x) = −x +1 −x −2= −2x −1 2) dla x €<−2,1) f(x) = −x +1 +x +2 = 3 3) dla x€<1,∞) f(x)= x−1 +x +2 = 2x +1 z wykresu odczytujemy ,że dla m€( −∞, 3) −−− brak rozwiązań( równanie sprzeczne) bo proste ( zielone f(m)=m −−− nie przecinają wykresu f(x) dodatkowo : dla m= 3 −− niesk, wiele rozwiązań −− równanie tożsamościowe dla m€(3,∞) dwa rozwiaząnia

Eta: poprawiam ( nie równanie ) tylko nierówność nie ma rozwiązań dla m€( −∞, 3)

blacha: Eta mam pytanie. |x−1|+|x+2|<m przy tej nierówności zauważ że |x−1|+|x+2| JEST < m a Nie ≤ m czyli rysując wykres to nasze 3 proste rysujemy standardowo liniami przerywanymi bo nie należą do M. Dla m =3 jest więc brak rozwiązań bo m nie należy do prostej x = 3 więc m∊ ( − niesk. , 3 >