Dowód, planimetria, okręgi.
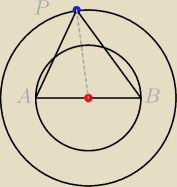
JeanJacob: Dane są dwa współśrodkowe okręgi. W mniejszym okręgu zaznaczono średnicę AB, na większym
wybrano punkt P. Wykaż że suma |PA|2+|PB|2 jest stała. Rozważ dwa przypadki
8 kwi 23:09
Adamm:
z tw. Cosinusów
|PA|
2=R
2+r
2−2*r*R*cosα oraz |PB|
2=R
2+r
2+2*r*R*cosα
skąd |PA|
2+|PB|
2=2R
2+2r
2
jeśli A, B, P są współliniowe
|PA|=R+r oraz |PB|=R−r lub odwrotnie
skąd |PA|
2+|PB|
2=2R
2+2r
2
zatem suma |PA|
2+|PB|
2 jest stała c. b. d. o.
8 kwi 23:29
Adamm: wiadomo czym jest R, r ale nie oznaczyłem α
mam nadzieję że się domyślisz o co chodzi
8 kwi 23:30
JeanJacob: dzięki, wszystko widać
9 kwi 19:55
 z tw. Cosinusów
|PA|2=R2+r2−2*r*R*cosα oraz |PB|2=R2+r2+2*r*R*cosα
skąd |PA|2+|PB|2=2R2+2r2
jeśli A, B, P są współliniowe
|PA|=R+r oraz |PB|=R−r lub odwrotnie
skąd |PA|2+|PB|2=2R2+2r2
zatem suma |PA|2+|PB|2 jest stała c. b. d. o.
z tw. Cosinusów
|PA|2=R2+r2−2*r*R*cosα oraz |PB|2=R2+r2+2*r*R*cosα
skąd |PA|2+|PB|2=2R2+2r2
jeśli A, B, P są współliniowe
|PA|=R+r oraz |PB|=R−r lub odwrotnie
skąd |PA|2+|PB|2=2R2+2r2
zatem suma |PA|2+|PB|2 jest stała c. b. d. o.