wykres homo:

	m
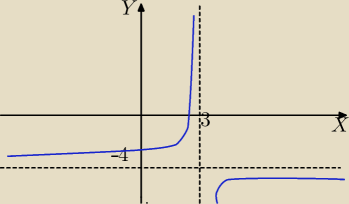
Punkt (4,−6) należy do wykresu funkcji f(x) =		+ b
	x−a

napisz wzór funkcji w postaci ilorazu dwu wielomianów pierwszego stopnia

	6 − 3x
i rozwiąż nierówność f(x) ≥
	x −3

Mila: Ustal wzór wg tego co zrobiłam wcześniej.

homo:

	m
f(x) =		−4
	x−3

homo: m = − 2

homo:

	10−4x
f(x) =
	x−3

i co dalej ?

Mila: Dobrze.

5-latek: Zle jest p dajesz zawszse ze zmienionym znakiem do wzoru masz p=3

	m
wiec f(x)=		−4= licz
	x−(−3)

5-latek: Ja napisalem zle (dobrze masz p=3 a nie p=−3

homo: tutaj nie ma p tylko a

homo:

	10−4x		6−3x		4−x
		≥		=>		≥ 0
	x−3		x−3		x−3

czyli (x−4)(x−3) ≤ ) => x ∊ [3,4]

Mila: x≠3

10−4x		6−3x
	≥		/*(x−3)2
x−3		x−3

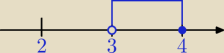
(10−4x)*(x−3)≥(6−3x)*(x−3)⇔ (10−4x)*(x−3)−(6−3x)*(x−3)≥0 (x−3)*(10−4x−6+3x)≥0 (x−3)*(−x+4)≥0 parabola skierowana w dół x∊(3,4>

homo: no tak 3 odpada dzięki