Stereometria, sześcian wpisany w ostrosłup Shakkozu: W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do wysokości ścian bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz stosunek objętości ostrosłupa do objętości sześcianu, jeżeli kąt nachylenia ściany bocznej do płaszczyzny podstawy jest równy α

Mila:

	H
tgα=		⇔H=0,5a*tgα
	0.5a

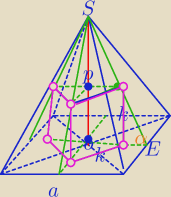
ΔSPM∼ΔSOE:

H−k		H		H*a
	=		⇔k=
0.5k√2		0.5a		H√2+a

	0.5a2tgα
k=		⇔
	0.5√2atgα+a

	a*tgα
k=
	√2tgα+2

V_sześcianu=k³

	1		a2*0.5a*tgα
VO=		*a2*H=
	3		3

Vsz		a3*0.5*tgα   3
	=		=
Vo		a3*tg3α   (√2tgα+2)3

	(√2tgα+2)3
=
	6tg2α

============= sprawdź rachunki, albo odpowiedź.