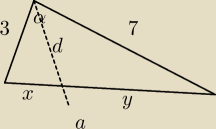
planimetria StrasznyNieogar: Dzieńdobry Ramiona trójkąta mają długość 3 i 7, a kąt między nimi 120 stopni. Wyznacz długość odcinka dwusiecznej kąta rozwartego zwartego w trojkącie. a=x + y tw. cosinusów: a² = 3² + 7² − cos120*2*3*7

	1
a2 = 9 + 49 +		*2*3*7
	2

a² = 79 a = √79 = x + y tw. o dwusiecznej kąta w trójkącie:

x		3
	=
y		7

	7x
y =
	3

	7x
x +		= √79
	3

10x = 3 √79

	3√79
x=
	10

tw. cosinusów:

	3√79
(		) = 32 + d2 − cos60 *2 *3 *d
	10

711
	= 9 +d2 − 3b
100

	189
d2 − 3d +		= 0
	100

	36
Delta mi wychodzi
	25

d1 = 9/10 d2 = 21/10 ===> taki jest wynik w odpowiedziach co z d1? Gdzie popełniłem błąd

'Leszek: Zrob to zadanie wykorzystujac pola trojkatow P₁ = 0,5*3*d sin 60° P₂ = 0,5*7*d sin 60° P_c = 0,5*3*7 sin 120° Oraz : P_c = P₁ + P₂

StrasznyNieogar: Wiem, wiem, ale bardziej mi chodzi o to czy autor zadania nie pomyślał o takim sposobie rozwiązania czy popełniłem błąd

Adamm: spróbuj nierówności trójkąta

StrasznyNieogar: to znaczy?

Adamm: y=7√79/10 tw. Cosinusów (7√79/10)²=d²+7²−2*d*7*cos60^o 0=d²−7d+10,29 Δ=49−41,16=7,84

	7±2,8
d=
	2

d=4,9 lub d=2,1 stąd mamy d=2,1 nie popełniłeś błędu, skończyłeś zbyt wcześnie

Pytający: 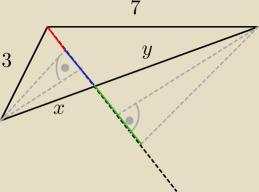9/10 21/10−9/10=12/10 49/10−21/10=28/10 Nic nie jest błędnego w Twoim liczeniu, ale jeśli zastosujesz twierdzenie cosinusów dla

	21		49
trójkąta z dwusieczną i igrekiem, wyjdzie Ci d=		⋁ d=		, stąd rozwiązaniem jest
	10		10

	21
d=		spełniające oba równania.
	10

StrasznyNieogar: Rozumiem, chłopaki o to chodziło Dzięki : )

StrasznyNieogar: Chociaż nigdy nie miałem tak w zadaniu i zdziwiło mnie to