Geometria analityczna MadZigZag: Znajdź równanie prostej równoległej do prostej o równaniu 3x+4y+1=0 i stycznej do okręgu o równaniu x²+y²−4x−2y+4==0 x²+y²−4x−2y+4=0 → (x−2)²+(y−1)²=2 P=(2,1) Czy w tym zadaniu mogę wyznaczyć sobie prostą 3x+4y+C=0 i policzyć ze wzoru na odległość puktu P od prostej o równaniu Ax+By+C? Próbuję robić tym sposobem i dziwne wyniki mi wychodzą tz C=5√2−10

Metis: Dwa sposoby: https://www.zadania.info/d1430/6339644

jc: IV sposób. Idziemy od punktu (2,1) w kierunku wektora (3,4) aż przetniemy okrąg. (3t)² + (4t)²=1, t = 1/5 (promień = 1, nie √2 jak wyżej) Punkty styczności: (2,1) ± 1/5 (3,4). Styczne: 3(x − 2 ± 3/5) + 4(y − 1 ± 4/5)=0.

Metis: Znalazłoby się pewnie i więcej

MadZigZag: dziekuję jestędebilę

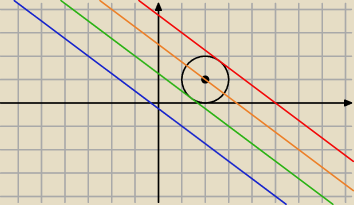
5-latek: Albo Piszsemy rownanie prostej rownoleglej do prostej 3x+4y+1=0 (niebieska ) i przechodzacej przez punkt S=(2,1) 3*2+4*1+C₁=0 C₁=−10 Rownanie tej prostej ma postac 3x+4y−10=0 (pomaranczowa Teraz ze wzoru na odleglosc dwoch prostych rownoleglych znajdziemy rownania prostych stycznych do okregu i rownoleglych do prostej 3x+4y+1=0

	|C2−C1|
d=
	√A2+B2

	|C2+10|
1=
	5

C₂+10=5 to C₂=−5 lub C₂+10=−5 to C−2= −15 Rownania naszych prostych stycznych sa takie 3x+4y−5=0 (zielona 3x+4y−15=0 (czerwona

5-latek: Mialo byc .....i rownoleglych do prostej 3x+4y−10=0