x Pan X: oblicz sumę wszystkich miejsc zerowych funkcji f(x)= cos(2x) gdzie x∊<0,100π>

Pan X: ktoś wie może przynajmniej jakie będzie największe miejsce zerowe i zarazem ≤100π? Tylko tego mi brakuje do szczęścia

Pytający:

	π		π		kπ
cos(2x)=0 ⇔ 2x=		+kπ ⇔ x=		+		, k całkowite
	2		4		2

	π		kπ		1		1
0≤		+		≤100π ⇒ −		≤k≤200−
	4		2		2		2

	π		kπ		π   0*π   π   199π   ( + )+( + )   4   2   4   2
∑(k=0 do 199)(		+		)=		*200=10000π
	4		2		2

Mila: cos2x=0 dla x∊<0,100π>

	π
2x=		+kπ /:2
	2

	π		2π
x=		+		*k
	4		4

π		3π		5π		399π
	,		,		,....,
4		4		4		4

liczymy:

π		2π
	+		*k≤100π
4		4

2π		π
	*k≤100π−
4		4

	π		4
k≤(100π−		)*
	4		2π

k≤199¹₂ i k∊N k=199

	π		2π		399π
ostatnie miejsce zerowe w przedziale : x=		+		*199=
	4		4		4

Pan X: a ile bedzie tych miejsc zerowych, mi wyszlo niby 799 ale nie wierze w to

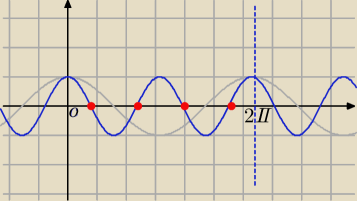
Mila: 1) No przecież masz policzoną sumę .Patrz wpis: u Pana Pytający− 22:20 : U mnie obliczone:

	π
x0=
	4

	399π
x199=
	4

Czyli masz 200 miejsc zerowych. albo 2) Bez tego liczenia , z rysunku. Popatrz na rysunek ; w każdym przedziale o długości 2π masz 4 miejsca zerowe. 50*4=200.

Pytający: Wystarczy "Patrz wpis Pytającego", Pani Milo.

Mila: Hej.

Pytający: Hej, hej!

Pan X: Dziękuję Wam