pochodna Panda: Wyznacz wszystkie wartości parametru m, dla ktorych równanie x³ − 3x + 2 = m f(x) = x³ − 3x + 2 − m = 0 f'(x) = 3x² − 3 = 3(x − 1)(x + 1) z wykresu pochodnej wynika, ze f(x) osiąga wartośc max = 4 i minimalną = 0 Co dalej mam z tym zrobić?

Jerzy: Jaka jest treść zadania ?

Panda: Treść zadania Wyznacz wszystkie wartości parametru m, dla ktorych równanie x³ − 3x + 2 = m ma dwa pierwiastki ujemne i jeden dodatni

Jerzy: Zacznij od rozłożenia na czynnki: (liniowy)* (kwadratowy). Znając znak pierwiastka dla liniowego , nałożysz warunki dla kwadratowego.

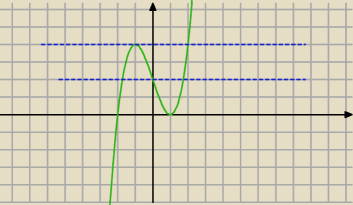
Jerzy: Niebieska linia, to : y = m Pomiedzy nimi są spełnione warunki zadania.

Jerzy: Nie traktuj postu 15:50 ( myslałem,że z prawej strony jest 0) Analizuj funkcję, pod kątem takiego szkicu.

Panda: Rzeczywiście już mam wzór f(x) = (x − 1)² (x+2) Narysowałem wykres tej funkcji, przecina oś OY w 2, miejsca zerowe to 1 i −2, ale w 1 nie przebija osi OX jak teraz wyznaczyc m?

Panda: Już widzę o co chodzi, dziękuje