Zadanie z pochodną Weronika: Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość a. Wyznacz taką wysokość ostrosłupa, dla której jego objętość jest największa i uzasadnij, że kąt między przeciwległymi krawędziami bocznymi jest rozwarty.

Jerzy: Z czym masz problem ?

Weronika: Jerzy, czy ty mógłbyś choć raz rozwiązać zadanie, jak cię ktoś o to prosi? A nie dręczyć i zadawać takie pytania, że jeszcze bardziej nie wie się o co chodzi? Czasami najlepiej rozumie się zadanie jak zobaczy się rozwiązanie. Nie traktuj każdego jak lenia, który przyszedł tu po to żeby spisać zadanie i nawet nie zastanowić się o co chodzi w rozwiązaniu. Pozdrawiam

Jerzy: Często rozwiązuję zadania, ale mimo wszystko jestem zwolenikiem pomagania (wspólnego rozwiazywania z autorem postu, bo to daje największą korzyśc).Podawanie rozwiazania "na tacy" nie jest dobrą metodą dydaktyczna. Chętnie Ci pomogę, bo po to jestem na forum , aby pomagać, a nie jak twierdzisz dręczyć kogokolwiek. Jestem daleki od tego.

Jerzy: Przez chwilę się zastanów, co potrzebujesz znać , aby obliczyć objetość tej bryly , a potem spróbuj ustalić , jak zanając krawędź boczna, wyznaczyć te wielkości. Ponadto treśc zadania już sugeruje, ze zmienna niezależna bedzie kat, jaki tworzy krawędź boczan z podstawą.

Weronika : Do wyznaczenia objętości potrzebna mi hest jedna niewiadoma. A tu mam 3 − krawędź boczną, krawędź podstawy i wysokość. Pitagoras mnie chyba jakoś specjalnie nie ratuje, dalej mam dwie niewiadome

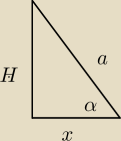
Jerzy: Spokojnie , już wyżej napisałem ,że wyrazimy objetość tej bryły tylko od jednej zmiennej. Popatrz na rysunek, jak sądzisz , co to jest x ( pamiętaj,że w podstawie jest kwadrat)

Weronika : X to połowa przekątnej

Jerzy: OK.

	H
Z trójkąta mamy:		= sinα ⇔ H = a*sinα ( czyli wysokość już mamy )
	a

x
	= cosα ⇔ x = a*cosα
a

Teraz zastanów się, jak znając x obliczyć krawędź podstawy.

Weronika : Jeżeli krawędź podstawy to np b, to x = b √2 / 2

Jerzy: Uważaj: x to połowa przekatnej podstawy, czyli kwadratu:

d
	= x = a*cosα ⇔ d = 2xcosα
2

no ale: d = k√2 ( gdzie k − krawędź podstawy ) k√2 = 2xcosα ..... i z tego oblicz k ( krawędź podstawy)

Jerzy: Trzecia linijka: d = 2acosα oczywiście Ostatnia: k√2 = 2acosα oczywiście.

ax: Można jeszcze dosypać garść papryki, posolić, popieprzyć ... i za okno wypieprzyć

Weronika : Ok, mam. Później już tylko podstawić do wzoru na objętość i policzyć pochodną?

Jerzy: Dokładnie tak, potem szukasz maksimum, obliczasz H ( takie było pytanie), na końcu uzasadnienie o kącie. Bolało ?

Tadeusz:

	x√2
y=
	2

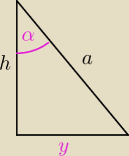
	x2
a2=h2+		⇒ 2a2=2h2+x2 ⇒ x2=2a2−2h2
	2

	1
V=		(2a2−2h2)*h
	3

	2		2
V=		a2h−		h3
	3		3

	2
V'(h)=		a2−2h2
	3

	2
V'(h)=0 ⇒		a2=2h2 ⇒ a2=3h2
	3

Weronika : Jeszcze nie koniec żeby oceniać czy bolało pochodna z ²₃ a³ sin α cos²α O ile dobrze wyliczyłam, to −4 a³ cos α sin α ? Czy warto zamieniać to na −2a³ sin 2α ?

Tadeusz:

	a
masz więc h=
	√3

	√3
Skoro tak to cosα=		jeśli nie chcesz odczytywać z tablic i tak określić kąt 2α
	3

	√6
to sinα=
	3

cos2α=cos²α−sin²α

	3		6		1
cos2α=		−		=−		cos2α<0 zatem kąt rozwarty
	9		9		3

Jerzy: Objetość dobrze, pochodna źle.

	2
V'(α) =		a3(cos3α − 2sin2αcosα)
	3

Przeanalizuj też sposób Tadeusza, może bardziej Ci odpowiada .