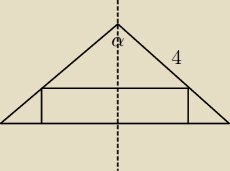
 Dany jest stożek o kącie rozwarcia 120 stopni i tworzącej długości 4. Oblicz objętość tego
walca wpisanego w dany stożek, którego pole powierzchni bocznej jest największe.
Dany jest stożek o kącie rozwarcia 120 stopni i tworzącej długości 4. Oblicz objętość tego
walca wpisanego w dany stożek, którego pole powierzchni bocznej jest największe.
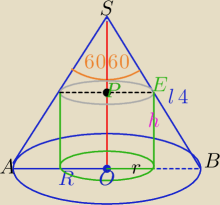 H=|OS|
H=2
H=|OS|
H=2
| 4√3 | ||
R= | =2√3 | |
| 2 |
| |SP| | H | |||
ΔSPE∼ΔSOB⇔ | = | |||
| |PE| | R |
| 2−h | 2 | ||
= | ⇔ | ||
| r | 2√3 |
| −2 | ||
Pmax dla h= | =1 | |
| −2 |
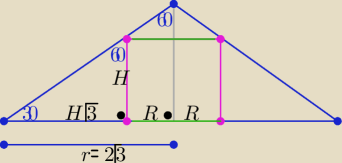 Można też tak ( z trójkąta "ekierki"
rst=2√3
Rw= 2√3−H√3=√3(2−H)
Pbw=2πRH ⇒ Pb(H)= 2π√3(−H2+2H) −−− osiąga max
Można też tak ( z trójkąta "ekierki"
rst=2√3
Rw= 2√3−H√3=√3(2−H)
Pbw=2πRH ⇒ Pb(H)= 2π√3(−H2+2H) −−− osiąga max
| −2 | ||
dla Hmax= | =1 to Rmax=√3 | |
| −2 |