funkcja magda: wyznac wartość najmniejsza i najwieksza funkcji kwadratowej f(x) = 2x² −5x + 3 w przedziale <−1,2>

Godzio:

	−(−5)		5
p =		=		∊ <−1,2>
	2*2		4

	5		25		25		50		25		12		37
f(		) = 2*		−		+ 3 =		−		+		=		= 9,25
	4		4		4		4		4		4		4

f(−1) = 2 +5 +3 = 10 −> największa f(2) = 8−10 +3 = 1 −> najmniejsza

magda: ale co to jest to p

magda: moglbys mi wytlumaczyc skad sie to wszytsko wzielo prosze

Godzio: już tłumacze

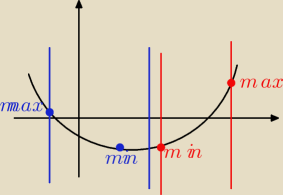
Godzio: f(x) = ax² + bx + c p to wierzchołek funkcji trzeba sprawdzić czy należy on do badanego przedziału :

	−b
p=
	2a

spójż na rysunek najpierw czerwony przedział, przykładowo <3,5> wierzchołek ( p ) nie należy do badanego przedziału, ale musimy to sprawdzić wyliczając go i patrząc na dany przedział jeśli nie należy do pomijamy go i sprawdzamy najmniejszą wartość i największą na końcach przedziału czyli liczymy f(3) i f(5) jeśli mamy funkcje f(x) = ax² + bx + c to f(3) = a*3² + b*3 + c = 9a + 3b +c i wyliczamy do końca mając a,b,c f(5) analogicznie to co wyszło większe jest największą wartością w tym wypadku f(5) > f(3) a f(3) jest najmniejszą 2 przypadek (niebieski przedział) przykładowo <−2,2> sprawdzamy czy wierzchołek należy, w tym wypadku należy więc liczymy f(p) , f(−2) , f(2) i wyliczamy największą i najmniejszą wartość, zrozumiałe ?

magda: teraz juz wiem.. ale i tam mam jeszcze jedno pyt... skoro nalezy tak jak w 2 przykladzie to w jakim celu sie liczy f(p) skoro i tak tego nie podajemy nigdzie

magda: i dlaczego tzreba sprawdzac czy przedzial nalezy do badanego przedzialu

magda: a nie wystarczylo by na przykladzie zadanie 1 poprostu tylko podstawic −1 i 2

Godzio: naczy trzeba sprawdzić czy wierzchołek należy do przedziału, a teraz widze że błąd zrobiłem z liczeniem wierzchołka

	5		25		25		50		100		48		2
f(		) = 2*		−		+3 =		−		=		= −		=
	4		16		4		16		16		16		16

	1
−
	8

czyli w tym wypadku wierzchołek przyjmuje najmniejszą wartością

magda: ale po co to sie sprawda

Godzio: dam przykład jeszcze jeden f(x) = 2x² + x − 1 x∊<−1,0> wierzchołek to najmniejsza wartość tej funkcji, ale musimy najpierw sprawdzić czy nalezy do przedziału w którym szukamy najmniejszej i najwięszej wartości;

	−b		−1		1
p=		=		= −		czyli p∊<−1,0>
	2a		4		4

trzeba teraz policzyć f(p) żeby podać tą najmniejszą wartość, i oprócz tego szukamy największej wartości więc wyliczamy wartości na końcu przedziałów

	1		1		1		1		2		8		9
f(−		) = 2*		−		−1 =		−		−		= −		−> minimum
	4		16		4		8		8		8		8

f(−1) = 2 −1 −1 = 0 −> max f(0) = 0 +0−1=−1 Dam Ci przykład do zrobienia jak chcesz to go zrób a ja go sprawdze f(x) = −x² + 2x + 5 x∊<0,3>

magda: aha teraz rozumiem... to f(p) liczy sie i potem nie zawsze sie okaze on najmniejsza czy najwieksza wart... ale atrzac co jest najwieksze czy najmiejjsze bierze tez sie to pod uwage... dobrze teraz mysle

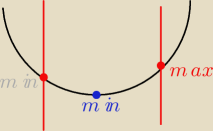
Godzio: bo jeśli należy do danego przedziału tzn że dla funcji z ramionami do góry osiągnie w przedziale najmnieszą wartość a dla funkcji z ramionami do dołu osiągnie wartość największą. Patrz na rusynek jeśli nie sprawdzimy czy wierzchołek nalezy do przedziału to wyjdzie nam że punkt po prawej będzie osiągał najmniejszą wartość co jest kompletną bzdurą. rozumiesz ?

Godzio:

	−b
Na samym początku liczy się p=		i sprawdza czy należy do przedziału jeśli tak to
	2a

dopiero wtedy liczy się f(p)

magda: p= 1 f(1)= −1 +2+5= 6 czyli nie nalezy do przedzialu f(0)=5 <−−− najwieksza f(3)= −9 +6+5= 2 <−−− najmniejsza dobrze

magda: zle juz poprawiam

magda: p= 1 nalezy wiec f(1)= 6 to jest najwieksza wart f(0)=5 f(3)= −9 +6+5= 2 <−−− najmniejsza

magda: teraz dobrze

Godzio: wszystko ok

magda: a i ja liczylam w ten sposob − (1)² bo gdyby bylo tak (−x)² to wtedy inaczej wychodzi

magda: no to dziekjue teraz juz wszytsko rozumie

Godzio:

nic: a co jeśli 'p' nie należy do przedziału?