geometria hol: Wykaż, że istnieje w trójkącie taka prosta, która dzieli jego pole i obwód na dwie równe części.

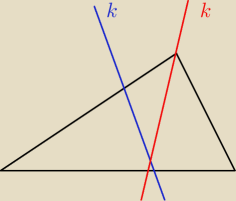
kochanus_niepospolitus: Na początek zauważmy, że prosta k może nasz trójkąt podzielić albo na dwa trójkąty (jeżeli przechodzi przez jeden z wierzchołków) albo na trójkąt i czworokąt 1) Jeżeli trójkąt jest równoramienny, to k zawiera wysokość trójkąta (pola oczywiście są podzielone na pół, tak samo obwód) 2) Jeżeli trójkąt nie jest równoramienny, to k nie może przechodzić przez wierzchołek trójkąta, ponieważ prosta musiałaby przechodzić przez środek podstawy (co by pola były równe), a wtedy obwody nie będą sobie równe (różne długości ramion) Tak więc, musi być trójkąt i czworokąt. Przez moment zastanów się nad tym, jak by to rozwiązać

g: Wyobraźmy sobie wszystkie proste które dzielą trójkąt na dwa równe pola. Ten zbiór jest ciągły, to znaczy że dla każdego kąta (każdego kierunku) da się znaleźć taka prosta. Jedna z tych prostych ma z lewej strony część obwodu L1 a z prawej L2. Teraz przesiadamy się na coraz to inną prostą, w sposób ciągły, zwiększając kąt kierunkowy. Po zmianie kąta kierunkowego o 180^o wrócimy do tej samej prostej, ale teraz z lewej będzie L2 a z prawej L1. To znaczy że gdzieś po drodze musiało być to samo z lewej i z prawej.

Jerzy: Są na to gotowe wzory: http://www.matematyka.wroc.pl/ciekawieomatematyce/polowiaca-i-pole-i-obwod-trojkata

Jerzy: Wszystko to prawda, ale ten tok rozumowania dotyczy oddzielnie obwodu , a oddzielnie pola. Problem w tym ,że obwód i pole mają być podzielone na pół jednocześnie tą prostą.

Jerzy: Chociaż nie ... masz rację, dwa trójkąty o tym samym obwodzie mają takie samo pole.

Adamm: Jerzy, "dwa trójkąty o tym samym obwodzie mają takie samo pole"