planimetria
ola: Dany jest trójkąt równoboczny ABC wpisany okrąg. Punkt P leży na krótszym łuku AC. Wykaz, że
PB= PA+PC
5 kwi 19:58
kochanus_niepospolitus:
Na jakim 'krótszym łuku' AC

5 kwi 19:59
kochanus_niepospolitus:
Napisz jeszcze raz całe zadanie ale teraz DOKŁADNIE

Bez żadnych inwencji twórczych
5 kwi 20:00
Adamm: kochanus, dla mnie zadanie jest zrozumiałe
wierzchołki A oraz C dzielą okrąg na dwa łuki
5 kwi 20:06
Saizou :
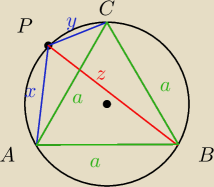
Z tw. Ptolemeusza mamy
az=ax+ay
z=x+y
c.k.d
5 kwi 20:07
ola: Dokladnie przepisalam zadania i fakt.. jak zaczęłam rozrysowywać to bzdura kompletna...
5 kwi 20:08
Eta:
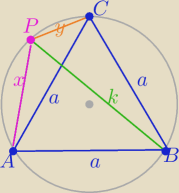 łuki mają tę samą długość
łuki mają tę samą długość
Z twierdzenia Ptolemeusza
|AC|*|PB|=|PA|*|BC|+|PC|*|AB| ponieważ |AB|=|BC|=|AC|=a >0
to |PB|*a=|PA|*a*|PC|*a / :a ⇒ |PB|=|PA|+|PC|
c.n.w
5 kwi 20:09
Saizou : 
5 kwi 20:11
ola: dzieki

5 kwi 20:12
5 kwi 20:13
Adamm:
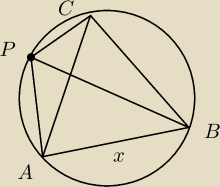
z tw. Cosinusów
|PB|
2+|PC|
2−2*|PC|*|PB|*cos60
o=x
2
|PB|
2+|PA|
2−2*|PA|*|PB|*cos60
o=x
2
|PB|*(|PA|−|PC|)=|PA|
2−|PC|
2
|PB|=|PA|+|PC|
c. b. d. o.
5 kwi 20:15
młodziutki: Wiem, że stare, ale wpadłem na fajny pomysł.
Przedłużamy odcinek PA w taki sposób, że kąt AKB to 60 stopni, (K to punkt który powstaje po
przedłużeniu) wtedy KBP to 60 więc równoboczny.
I nasza teza sprowadza się do AK = PC. ale trójkąt AKB i CPB są przystające. c.k.d
6 lut 20:17
.: Zastanów się nad tym co napisałeś.
Skoro przedłużamy AP i mamy kat AKB = 60° to kat KBA < 60° (Zauważ że kat BAK > kat BAC =
60°), więc kat KBP < 60°
Niewspominajac już o tym że w jakim wszechświecie kat BPK według Ciebie mógłby być rowny 60° ?
Można szybko wykazać że kat BPA będzie kątem ostrym związku z tym kat BPK będzie kątem
rozwartym.
6 lut 20:57
.:
Teraz widzę w którą strone chcesz przedłużać odcinek PA.
6 lut 21:06
młodziutki: BCA = BPA = BPK = 60. Oparte na tym samym łuku. A skoro przyjeliśmy, że AKB 60 to KBP to 60.
Chyba ciebie nie zrozumiałem jak masz siłę to możesz próbować mi wytłumaczyć.
6 lut 21:08

 Bez żadnych inwencji twórczych
Bez żadnych inwencji twórczych
 Z tw. Ptolemeusza mamy
az=ax+ay
z=x+y
c.k.d
Z tw. Ptolemeusza mamy
az=ax+ay
z=x+y
c.k.d
 łuki mają tę samą długość
Z twierdzenia Ptolemeusza
|AC|*|PB|=|PA|*|BC|+|PC|*|AB| ponieważ |AB|=|BC|=|AC|=a >0
to |PB|*a=|PA|*a*|PC|*a / :a ⇒ |PB|=|PA|+|PC|
c.n.w
łuki mają tę samą długość
Z twierdzenia Ptolemeusza
|AC|*|PB|=|PA|*|BC|+|PC|*|AB| ponieważ |AB|=|BC|=|AC|=a >0
to |PB|*a=|PA|*a*|PC|*a / :a ⇒ |PB|=|PA|+|PC|
c.n.w


 z tw. Cosinusów
|PB|2+|PC|2−2*|PC|*|PB|*cos60o=x2
|PB|2+|PA|2−2*|PA|*|PB|*cos60o=x2
|PB|*(|PA|−|PC|)=|PA|2−|PC|2
|PB|=|PA|+|PC|
c. b. d. o.
z tw. Cosinusów
|PB|2+|PC|2−2*|PC|*|PB|*cos60o=x2
|PB|2+|PA|2−2*|PA|*|PB|*cos60o=x2
|PB|*(|PA|−|PC|)=|PA|2−|PC|2
|PB|=|PA|+|PC|
c. b. d. o.