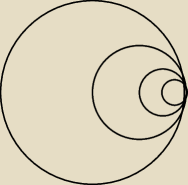
koło bbbb: Dany jest okrąg o1 o promieniu r . Wewnątrz tego okręgu narysowano okrąg o2 styczny wewnętrznie o średnicy r , wewnątrz okręgu o2 znów narysowano okrąg styczny wewnętrznie o średnicy 1/2 r itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę wszystkich w ten sposób utworzonych okręgów. Ogólnie to potraktowałem to jako szereg geometryczny: q=πr/2πr=1/2=(1/2πr)/πr=(1/4πr)/(1/2πr) S=2πr/(1−1/2)=2πr/(1/2)=2πr*2=4πr dobrze jest?

kochanus_niepospolitus: oblicz sumę (czego) wszystkich w ten sposób utworzonych okręgów Masz rację ... będzie to ciąg geometryczny

bbbb: sorki, zapomnałem napisać, że chodzi oczywiście o sumę długosci wszystkich okręgów

kochanus_niepospolitus: rozwiązanie ... ok