Trudne zadanie zimnygrzejnik: Odcinki o długościach: 2*√3, 3−√3,3*√2 są bokami trójkąta. a) Wyznacz miarę największego kąta tego trójkąta i oblicz długość wysokości poprowadzonej z wierzchołka tego kąta. b) Oblicz długość promienia okręgu opisanego na tym trójkącie.

Jack: a) najwiekszy kat lezy na przeciwko najdluzszego boku trojkata

zimnygrzejnik: Obliczyłem już kąt (wyszło 60 stopni), ale wysokość mi wychodzi nie za fajna

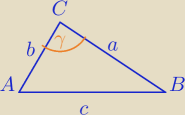
Mila: 1) (3−√3)²=9−6√3+3=12−6√3 (3√2)²=9*2=18 (2√3)²=4*3=12⇔ 3√2>2√3>3−√3 c=3√2 a=2√3, b=3−√3 2) c²=a²+b²−2*a*b*cosγ 18=12+12−6√3−2*2√3*(3−√3)*cosγ −6+6√3=−4*√3*(3−√3) cosγ −6+6√3=(−12√3+12)*cosγ −6(1−√3)=12(−√3+1)*cosγ

	1
cosγ=−
	2

γ=180^o−60^o γ=120^o 3) R

c
	=2R
sin(120o)

3√2
	=2R
√3   2

licz