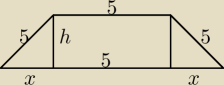
optymalizacja StrasznyNieogar: Rozpatrujemy wszystkie trapezy równoramienne, w których długość krótszej podstawy i długości ramion są równe 5 . Oblicz długość dłuższej podstawy tego z rozpatrywanych trapezów, który ma największe pole.Oblicz to pole. Co robię źle?

	1
P=		(a+b)h
	2

h² + x² = 5² x² = 25 − h² x=√25 − h² 2x=2 * √25 − h² = √100 − 4h² Dłuższa podstawa = 5 + √100 − 4h²

	1
P(h)=		(5 + √100 − 4h2 + 5)h = 10h + √100h2 − 4h4 ==== > dałem h pod pierwiastek
	2

0<h<5

	1
P'(h) =		(10 + 200h − 16h3) = −8h3 + 100h +5
	2

tu juz cos zle napewno Ktoś coś?

StrasznyNieogar: ?

Eta:

	2x+5+5
a=2x+5 , b= 5 , h= √25−x2 , x∊(0,5) P=		*h
	2

P(x)=(5+x)(√25−x²

	(5+x)*(−2x)
P'(x)= 1*√25−x2 +
	2√25−x2

P^'(x)=0 ⇒ 25−x²−(5+x)*x =0 dokończ................

	5
x=		to a= 10 i P=...
	2

Taki trapez składa się z trzech trójkątów równobocznych o boku 5

	52√3		75√3
P= 3*		=		[j2]
	4		4

StrasznyNieogar: A mój sposób jest zły?

kochanus_niepospolitus: źle policzona pochodna:

	1
p(h) =		(10h + √100h2 − 4h4)
	2

	1		−1
p'(h) =		(10 +		*(200h − 16h3))
	2		2√100h2 − 4h4

StrasznyNieogar: Jak to zrobiłeś?

StrasznyNieogar: Ok juz wiem, czyli warto się nauczyć pochodna funkcji zlozonej do matury Chyba ze inaczej idzie wybrnąć z tej sytuacji

kochanus_niepospolitus: