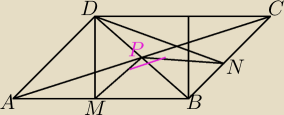
Równoległobok i cosinus ABCD: Dobry wieczór, mógłby ktoś pomóc mi z zadankiem ? W równoległoboku ABCD przekątne AC i BD przecinają się w punkcie P. Z wierzchołka D kąta rozwartego równoległoboku poprowadzono wysokości DM i DN(jak na rysunku obok). Wiadomo, że sinus kąta ostrego równoległoboku jest równy 0,8. Wyznacz cosinus kąta (wypukłego) MPN. Bardzo proszę o pomoc!

ABCD: Proszę proszę!

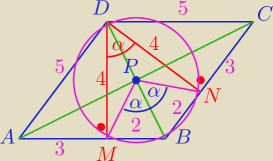
Janek191: Może równoległobok ABCD jest rombem ?

Iga: Jak w takim razie policzyć kąt alfa?

a7: kąt MPN =2α sin2α=2sinαcosα sinα=8/10 to cosα=√1−64/100=6/10 czyli sin2α=2*8/10*6/10=24/25 czyli cos2α=−√1−576/625=−7/25 (minus gdyż w drugiej ćwiartce cosinus jest ujemny)