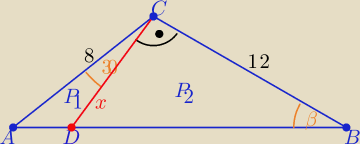
geometria płaska massdenim98: W trójkącie ABC AC=8, BC=12 a kąt ACB=120 stopni. Przez wierzchołek C poprowadzono prostą prostopadłą do boku BC. Przecięła ona bok AB w punkcie D. Oblicz: długość odcinka CD promień okręgu opisanego na trójkącie ABC

Eta:

	1
P(ABC)=		*8*12*sin120o ⇒ P=24√3
	2

	1
P1=		*x*8*sin30o ⇒ P1=2x
	2

	x*12
P2=		= 6x
	2

P₁+P₂=P⇒8x=24√3 ⇒ x=|CD|= 3√3

	8
Z tw. sinusów w ΔABC : 2R=
	sinβ

	12
W ΔDCB : sinβ=		, |DC|=√122+x2=..... to sinβ=.....
	|DC|

R= ...... dokończ..........