geometria płaska
massdenim98: W trójkącie ABC o bokach AB=10, BC=8, AC=6 poprowadzono prostą DE równoległą do boku AC
(punkt D leży na odcinku AB a punkt E na odcinku BC). Znajdź długość odcinków DB i EB,
jeżeli prosta DE podzieliła trójkąt ABC na figury o równych polach
4 kwi 22:46
Adamm:
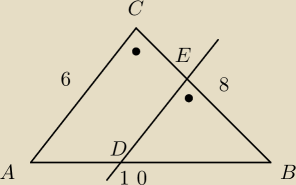
trójkąty ABC oraz DBE są podobne na zasadzie kkk
k=
√PDBE/PABC=
√2/2
|DB|=k*10=5
√2
|EB|=k*8=4
√2
4 kwi 22:57
Milo:
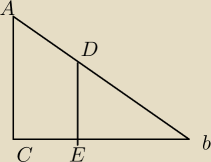
Zauważmy, że trójkąt BDE jest podobny do trójkąta BAC (te same kąty).
Wiemy też, że P
BDE = P
ACED oraz P
BDE+P
ACED = P
BAC, skąd
Jeśli trójkąty są podobne w skali k, to ich pola są podobne w skali k
2.
| | √2 | |
|DB| = k*|AB| = |
| * 10 = 5√2 |
| | 2 | |
| | √2 | |
|EB| = k*|CB| = |
| * 8 = 4√2 |
| | 2 | |
4 kwi 22:59
massdenim98: dzięki piękne
4 kwi 23:06
 trójkąty ABC oraz DBE są podobne na zasadzie kkk
k=√PDBE/PABC=√2/2
|DB|=k*10=5√2
|EB|=k*8=4√2
trójkąty ABC oraz DBE są podobne na zasadzie kkk
k=√PDBE/PABC=√2/2
|DB|=k*10=5√2
|EB|=k*8=4√2
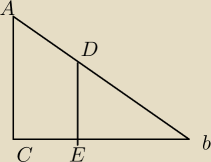 Zauważmy, że trójkąt BDE jest podobny do trójkąta BAC (te same kąty).
Wiemy też, że PBDE = PACED oraz PBDE+PACED = PBAC, skąd
Zauważmy, że trójkąt BDE jest podobny do trójkąta BAC (te same kąty).
Wiemy też, że PBDE = PACED oraz PBDE+PACED = PBAC, skąd