prostokąt basiulek: obwód prostokąta jest równy 8. Wyznacz długości jego boków, tak aby prostokąt miał jak najkrótszą przekątną

basiulek:

Adamm: x, y <− boki x+y=4 d=√x²+y²=√x²+(4−x)² f(x)=x²+(4−x)² mamy minimum dla x=2 taki prostokąt jest kwadratem

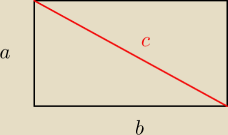
Jack: 2a + 2b = 8 a + b = 4 −−−> a = 4 − b założenia : a>0, b ∊ (0;4) c² = a² + b² c² = (4−b)² + b² c² = 16 − 8b + 2b² c(b) = √16−8b+2b²

	4b − 8		2b−4
c ' (b) =		=
	2√16−8b+2b2		√16−8b+2b2

c ' (b) = 0 2b − 4 = 0 −−> b = 2 a = 2 jest to kwadrat.