Optymalizacja KML: Dany jest trojkąt prostokatny o przyprostokatnych a i b , a+b=10. W trojkat wpisano kwadrat w taki sposób, ze dwa jego boki zawieraja sie w przyprostokatnych. Ustal długosci boków trojkata tak, aby wpisany w niego kwadrat mial najwiesze pole.

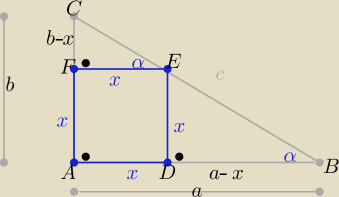
Eta: Z podobieństwa trójkątów DBE i ABC z cechy (kkk)

a−x		a		ab
	=		⇒ x=		i z treści zadania a+b=10 ⇒ b=10−a , a∊(0,10)
x		b		a+b

	ab		1
to x=		=		a*(10−a)
	10		10

Pole kwadratu jest największe jeżeli długość boku kwadratu jest największa

	1
x=−		a2+a −−− osiąga wartość największą dla odciętej wierzchołka paraboli
	10

	−1
czyli amax=		= 5 to bmax= 10−5=5
	−2/10

Taki trójkąt jest trójkątem prostokątnym równoramiennym : a=b=5 i c=5√2