Ekstrema Księżna Łucja: Wyznacz ekstrema i przedziały monotoniczności funkcji:

	x
f(x)=
	x2+1

Z góry dziękuje

Jack: A samemu cos? Oprocz dziekuje? 1. Dziedzina funkcji 2. Pochodna

Michał :): 1. Dziedzina. 2.Pochodna. 3.Przyrównujesz do zera. 4.Na podstawie wykresu przedziały monotoniczności i ekstrema . Powodzenia !

Księżna Łucja: Df=Df'=R

	−x2+1		−(x−1)(x+1)
f(x')=		=
	(x2+1)2		(x2+1)2

−(x−1)(x+1)=0 x₀=1 lub x₀=−1

Jack: Ok teraz krzywa przexhodzaca przez pubkty −1,1 oraz ze mamy minus to idzie od dolu. No a jako ze przez dwa punkty przechodzi to jest to parabola skierowana ramiona w dol.

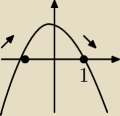
Księżna Łucja: I wychodzi maximum w −1 a minimum w 1 dobrze myśle ?

zef: Jeżeli to jest wykres pochodnej i wszystko się zgadza to w f(1) mamy maksimum a w f(−1) minimum

Jack: No i najlepiej to troszke rozpisac: Dla x ∊(−∞;−1) f'(x)<0 f↑ Dla x ∊(−1;1) f'(x)>0 f↑ Dla x ∊(1;∞) Dokoncz. I z tego mozna miec wniosek odnosnie ekstremow. Gdyz funkcja zmienia znaki Zatem mamy max lokalne w 1 i wynosi f(1) =... Mozna to zapisac np. tak f_max (1) =... I teraz minimum f_min (−1) =...

i: Ten temat został założony ze względu na to że maksimum i minimum często podaje odwrotne. I szczerze dalej nie wiem dlaczego dla x∊(1,∞) f'(x)<0 funkcja malejąca

Księżna Łucja: Nie wiem co jest źle na wykresie kilka postów wyżej

Księżna Łucja: Ok,już wiem on jest niedokładny bo nie rozpatrywane były przedziały tylko zaznaczane były elementy ,które "wydawały" się rosnące lub malejące ehh

Jack: oczywiscie co do tej monotonicznosci tam zle napisalem... dla x ∊ (−1;−1) f'(x) < 0 f↓ reszta ok, no przedzialy, przedzialy, a nie sam punkt