funkcja optymalizacja 2k17: Rozpatrujemy wszystkie prostokąty ABCD , których dwa wierzchołki A i B leżą na odcinku o końcach (0,0) i (4 ,0) , a dwa pozostałe wierzchołki C i D leżą na paraboli o równaniu 1 2 y = 2x − 2 x Oblicz obwód tego z rozpatrywanych prostokątów, którego pole jest największe.

Jerzy: Jakoś nie widać tu paraboli , widać za to funkcję stałą: y = 0

2k17: Mój błąd, jes to funkcja o równaniu y= −(1/2)x² + 2x

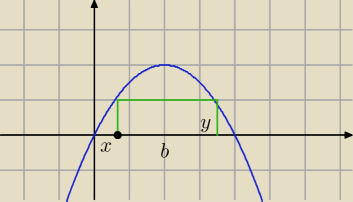
Jerzy: P = b* y b = 4 − 2x

	1
y = −		x2 + 2x
	2