Optymalizacja KML: Trojkąt rownoramienny o obwodzie p obraca się wokół podstawy. Jakie wymiary powinien miec trojkat, aby powstała w ten sposób bryła o najwiekszej objetosci. Wyznacz ją.

Jerzy:

	2		y
V =		πh2
	3		2

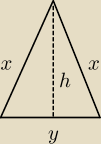
2x + y = p Wyznacz związek pomiedzy x i y i szukaj maksimum tej funkcji.

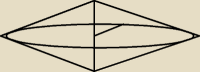
Adamm: masz 2 stożki o promieniu podstawy równej wysokości trójkąta, i tworzącej równej ramieniu p=2h+2l ⇒ h=p/2−l r=√l²−h²=√l*p−p²/4

	2		2		2
V=		πr2*h=		π(l*p−p2/4)*(p/2−l)=		p*π*(3l*p/4−p2/8−l2)
	3		3		3

mamy wierzchołek dla l=3p/8

	1
V=		πp2
	96

piotr: powinno p wystąpić w trzeciej potędze: p³

piotr:

	π p3
V =
	96