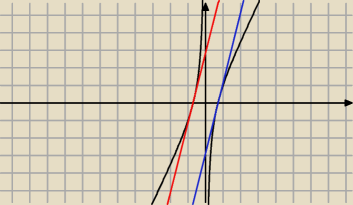
równania stycznych Dominikaaa: Znajdź równania stycznych do wykresu funkcji f(x)=2x2−1/x (x to mianownik ułamka) z ktorych każda styczna razem z osiami układów współrzędnych ogranicza trójkąt o polu 1 Proszę o wytłumaczenie zadania krok po kroku

piotr: czy to taka funkcja?

	2x2−1
f(x) =
	x

Dominikaaa: tak, to taka funkcja

piotr: wartośc pochodnej w punkcie x₀:

	1
f'(x0) =		+2
	x02

równanie stycznej w x₀

	1		2 x02−1
y(x) = f'(x0)(x − x0) + f(x0) ⇒ y(x) = (		+2)(x − x0) +
	x02		x0

	1		2 x02−1
y(0)= (		+2)(− x0) +		, |y(0)| ← wysokość trójkąta
	x02		x0

miejsce zerowe stycznej: y(a) = 0

	1		2 x02−1
(		+2)(a − x0) +		=0
	x02		x0

	2x0
⇒ a =		|a|← podstawa trójkąta
	2x02+1

Pole trójkąta:

	2x0		1		2 x02−1
P(x0) = a* y(0)/2 = −(		)((		+2)(− x0) +		)/2
	2x02+1		x02		x0

z warunku zadania P(x₀) =1

	2x0		1		2 x02−1
−(		)((		+2)(− x0) +		)/2 = 1
	2x02+1		x02		x0

⇒2 x₀²=1 ⇒ x₀ = −1/√2 lub x₀ = 1/√2 Styczne: y = 4 x + 2√2, y = 4 x − 2√2

piotr: