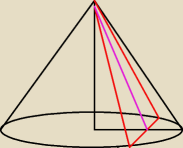
stożek kaisa: Stożek o wysokości 4 i promieniu podstawy 6 przecięto płaszczyzną przechodzącą przez wierzchołek stożka i cięciwę podstawy nie będącą średnicą. Pole otrzymanego przekroju jest równe 6. Wyznacz długość cięciwy. Proszę o pomoc : zrobiłam taki rysunek czerwony to przekrój, jednak nie wiem jak się dalej do tego zabrać

weronika: proszę o pomoc

Mila: Ładny rysunek zrobiłaś, ale bez oznaczeń. Poczekaj to po kolacji pomogę.

weronika: dziękuję bardzo! męczę się z tym i nic nie mogę zrobić w takim razie czekam na pomoc :3

weronika: Mila, to mogę liczyć na pomoc?

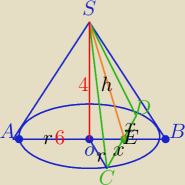Mila: H=4 r=6 P_ΔCDS=6

	1
6=		*2x*h
	2

x*h=6 W ΔSOC: |SC|²=4²+6²=52 W ΔSEC: |SC|²=x²+h² x²+h²=52 i x*h=6 i x∊(0,3)

	6
h=
	x

	6
x2+(		)2=52
	x

	36
x2+		=52 /*x2
	x2

x⁴−52x²+36=0 x²=t,t>0 t²−52t+36=0 Δ=2560=10*256=10*2⁸ √Δ=2⁴√10=16√10

	52−16√10		52+16√10
x2=		lub x2=
	2		2

x²=26−8√10 lub x²=26+8√10>3² nie odpowiada war.zadania x=√26−8√10 x=√(4−√10)² x=4−√10 ========

weronika: o jejku, dziękuję <3 A wiedziałabyś moze jak zrobić te zadania ? 1.Dany jest ostrosłup prawidłowy trójkątny. Stosunek długości krawędzi podstawy do krawędzi bocznej ostrosłupa jest równy 2:5. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa 2. Kąt rozwarcia stożka ma miarę 2alfa, pole jego powierzchni bocznej jest równe 12pi. Wyznacz objętość stożka. i w tym mam: Pb= 12pi r*l=12 l=12/r i chciałam to z sina = r/l ale nie wiem jak doprowadzić do końca

weronika: w razie czego proszę nawet o jakieś wskazówki

Mila: Jeżeli masz odpowiedzi to podaj.

weronika: nie mam niestety

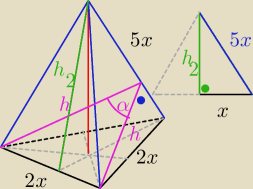Jack: 1. wyznaczymy kat z tw. cosinusow, jednak brakuje nam danej, ktora nazwalem "h" bo jest to nic innego jak wysokosc trojkata tworzacego sciane boczna. zatem wykorzystajmy pole sciany bocznej do tego wprowadzmy wysokosc h₂

	1
wtedy pole sciany bocznej to nic innego jak P =		* (2x) * h2 = x * h2
	2

Pole mozemy wyrazic rowniez przez "h"

	1		5
wtedy P =		* h * 5x =		h * x
	2		2

oba te pola opisuja te same pole − mianowicie sciane boczna, zatem sa sobie rowne. stad

	5
x * h2 =		h * x
	2

	5
h2 =		h
	2

jestesmy prawie w domu. Bo zostalo nam jakos wyznaczyc "h₂" za pomoca "x" ale od czego jest stary dobry pitagoras? przeciez sciana boczna, ktora ma wysokosc h₂ i podstawe 2x oraz krawedz boczna 5x spelnia rownanie (h₂)² + x² = (5x)² (x² a nie (2x)² bo polowa sciany bierze w tym udzial, patrz rys. u gory po prawej)

	5
wstawiajac za h2 − >		h
	2

25
	h2 + x2 = 25x2
4

25
	h2 = 24x2
4

	4		96
h2 = 24 *		x2 =		x2 (zauwaz,ze nie musimy znac "h",potrzebujemy jedynie h2)
	25		25

no i teraz twierdzenie cosinusow. (2x)² = h² + h² − 2*h*h * cos α 4x² = 2h² − 2h² cos α 2h² cos α = 2h² − 4x²

	2h2 − 4x2		4x2		2x2		2x2
cos α =		= 1 −		= 1 −		=1 −		=
	2h2		2h2		h2		96   x2 25

	2*25
= 1 −		= ...
	96

Jack: tam w pitagorasie bierze udzial polowa krawedzi podstawy* sorki za literowki, jesli jakies jeszcze beda

weronika: Dziękuję a jeśli chodzi o to 2 zadanie to co dalej trzeba byłoby zrobić?

Jack: te zadania sa na poziomie rozszerzenia z tego co widze , a wiec... ? : D

weronika: no na poziomie r. dlatego doszłam do pewnego momentu ale dalej nie wiem jak wybrnąć

Mila: Powinno być dobrze. (2) Jack piszesz, czy napisać?

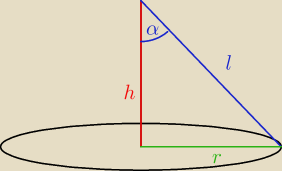Jack: 2. Kąt rozwarcia stożka ma miarę 2alfa, pole jego powierzchni bocznej jest równe 12π. Wyznacz objętość stożka. P_b = 12 π = π r l r*l = 12

	12
r =
	l

oraz

	r
sin α =
	l

czyli

	12   l		12
sin α =		=
	l		l2

	12
zatem l2 =
	sin α

obliczmy r², bedzie potrzebny do pitagorasa.

	12		144		144		144 sinα
skoro r =		to r2 =		=		=		= 12sinα
	l		l2		12   sin α		12

z pitagorasa h² = l² − r²

	12		1		1−sin2α		cos2α
h2 =		− 12sinα = 12(		− sinα) = 12(		)=12
	sin α		sinα		sinα		sinα

	cos2α
h = 2√3 * √
	sinα

objetosc :

	1		1		cos2α
V =		π * r2 * h =		π * 12sinα * 2√3 * √		= ...
	3		3		sinα

*sorki jesli cos skopalem

Jack: Milu jesli zrobilem zle to usun i napisz poprawnie ja tymczasem musze leciec.

Mila: Dobrze Jack, mam takie same wyniki pośrednie. .

	cosα
V=4π sinα*2√3*
	√sinα

V=8√3π*√sinα*cosα ================= Weroniko,licz wszystko po kolei jeszcze raz dla pewności.

Jack: