Oblicz pole i współrzędne wierzchołków Weronika: w okrąg o równaniu x² + y² − 4x −8y −5 = 0 wpisany jest trójkąt ABC, którego wierzchołki A i B należą do osi Ox. Bok BC trójkąta jest pięć razy dłuższy od boku AC. Oblicz pole trójkąta i współrzędne jego wierzchołków, wiedząc, że kąt trójkąta przy wierzchołku A jest rozwarty.

powrócony z otchłani: I w ktorym momencie natrafiasz na problem?

Weronika : Wyznaczenie współrzędnych wierzchołka C,i nie wiem w jaki sposób mogłabym tu wykorzystać informację że bok |BC| = 5|AC|.

kochanus_niepospolitus: np. możesz to wykorzystać w taki sposób: 1) A −− środek okręgu o promieniu 'r' 2) B −− środek okręgu o promieniu '5r' 3) Twój wstępny okrąg Trzy równania ... trzy niewiadome (x,y,r) rozwiązujesz i masz współrzędne punktu C (x,y) oraz dlugość boków AC i BC

kochanus_niepospolitus: ale taka uwaga ... czy aby na pewno dobrze napisałaś równanie tegoż okręgu?

Weronika : Tak równanie okręgu jest dobrze przepisane

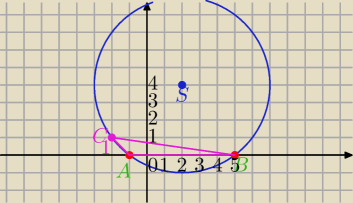
Mila: x² + y² − 4x −8y −5 = 0⇔ (x−2)²+(y−4)²=25 1) y=0 (x−2)²+4²=25 (x−2)²=9 x−2=3 lub x−2=−3 x=5 lub x=−1 A=(−1,0),B=(5,0) 2) C=(x,y) i C∊okręgu |BC| = 5|AC|⇔ {(x−5)²+y²}=5√(x+1)²+y² i x² + y² − 4x −8y −5 = 0 są dwa rozwiązania.

Mila: Ma być: √(x−5)²+y²=5*√(x+1)²+y²