| 3 | ||
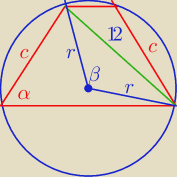
równy | , a przekątna ma długość 12. | |
| 4 |

| 3 | √7 | |||
sin α = | ⇒ cos α = √1 − sin2α = √ 1 − 916 = √ 716 = | |||
| 4 | 4 |
| 3 | √7 | 3 | ||||
sin β = sin 2α = 2 sin α* cos α = 2* | * | = | √7 | |||
| 4 | 4 | 8 |
| 1 | ||
cos β = √ 1 − 6364 = | ||
| 8 |
| 1 | ||
144 = 2 r2 − | r2 | |
| 4 |
| 7 | 4 | ||
r2 = 144 / * | |||
| 4 | 7 |
| 144* 4 | ||
r2 = | ||
| 7 |
| 24 | 24 | |||
r = | = | √7 | ||
| √7 | 7 |

| 12 | |
=2R | |
| sinα |
| 6 | |
=R | |
| 34 |