wyznacz równanie prostej do wykresu funkcji dfsdfs: Wyznacz rownanie prostej, której wykres jst prostopadly do wykresu funkcji −x+2y+6=0 i przechodzi przez punkt A=(−1,2)

Eta: k: −x+2y+6=0 w postaci kierunkowej

	1
k: y=		x−6
	2

p⊥k i A∊p to p: y= −2(x+1)+2 ⇒ p: y=−2x

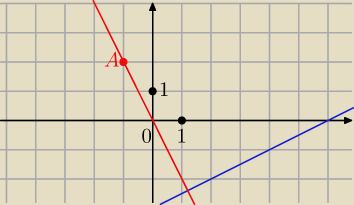
Janek191: − x + 2 y + 6 = 0 2 y = x − 6

	1
y =		a − 3
	2

więc prosta prostopadła ma równanie y = − 2 x + b i A = ( − 1, 2) więc 2 = 2 + b ⇒ b = 0 Odp. y = − 2 x =========

'Leszek: Prosta l: −x + 2y + 6 = 0⇒ y = 0,5x − 3 Prosta k ⊥ : y = − 2x + b i A= (−1, 2) dokoncz !

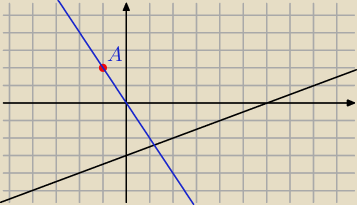
Powracający: 2y= x−6 y= 0,5x−3 a= 0,5 to a₁= −2 y= a₁(x+1)+2 y= −2(x+1)+2 y= −2x ========