dowód Michał :): Wykaż że dla dowolnych ujemnych liczb rzeczywistych ,,x'' i ,,y'' takich że x²+y²=1 , prawdziwa jest nierówność x+y≥−√2

Adamm: można to zrobić geometrycznie

Michał :): Mhmm , a jak to zrobic pisemnie ? w 1 zrobiłęm że to jest (x+y)² −2xy=1 potem przeniosłem 2xy ale to mnie do niczego nie prowadzi

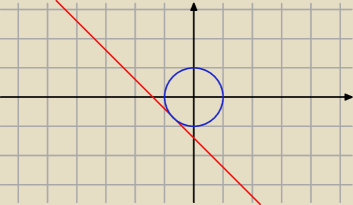
Adamm: prosta x+y+√2=0 jest styczna do okręgu x²+y²=1 jest ona pod okręgiem, więc biorąc dowolny punkt na okręgu zachodzi nierówność x+y+√2≥0

Michał :): Fajny sposób nie powiem i dzięki za to ale czy dałbyś rade to wytłumaczyć ,,metodą pisaną'' (jeżeli owy przykład da się tak zrobic )

Mariusz: x=cos(θ) y=sin(θ)

	1		1
cos(θ)+sin(θ)=√2(		cos(θ)+		sin(θ))
	√2		√2

	π
cos(θ)+sin(θ)=√2sin(		+θ)
	4

	π
cos(θ)+sin(θ)=√2sin(		+θ)
	4

Jakie jest najmniejsza wartość funkcji

	π
√2sin(		+θ)
	4

Adamm: da się taki sposób jest fajny x=sint, y=cost teraz podstawiasz i wzór sinx+cosx=√2sin(x+π/4)

Michał :): Dziękuję