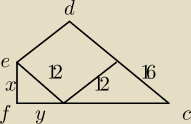
 Na zewnątrz trójkąta prostokątnego ABC, w którym |∢ACB|=90∘ oraz |AC|=12, |CB|=16 zbudowano
kwadrat ACDE (patrz rysunek). Punkt F leży na prostej AB i kąt |∢EFA|=90∘. Oblicz pole
trójkąta FAE.
Z twierdzenia Pitagorasa, w trójkącie ABC:
122+162=c2
144+256=c2
c2=400|√
|c|=√400=20
1. Czemu tutaj licze tangens a nie sin?
I potem mam takie coś
x/12= 12/ |AB|
x/12= 12/ 20 |⋅12
i tego działania też nie rozumiem jak to złożyć
dzięki za odp
Na zewnątrz trójkąta prostokątnego ABC, w którym |∢ACB|=90∘ oraz |AC|=12, |CB|=16 zbudowano
kwadrat ACDE (patrz rysunek). Punkt F leży na prostej AB i kąt |∢EFA|=90∘. Oblicz pole
trójkąta FAE.
Z twierdzenia Pitagorasa, w trójkącie ABC:
122+162=c2
144+256=c2
c2=400|√
|c|=√400=20
1. Czemu tutaj licze tangens a nie sin?
I potem mam takie coś
x/12= 12/ |AB|
x/12= 12/ 20 |⋅12
i tego działania też nie rozumiem jak to złożyć
dzięki za odp
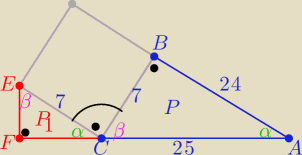 |AC|=...=25
|AC|=...=25
| 7 | ||
trójkąty EFC i ABC są podobne z cechy (kkk) w skali k= | ||
| 25 |
 Pewnie nie sa to tanie rzeczy .
Pewnie nie sa to tanie rzeczy .
 Pozdrawiam
Pozdrawiam 

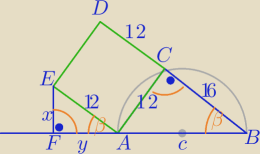 AE || DB
|AB|=c=20 z tw. Pitagorasa
∡FAF≡∡ABC
AE || DB
|AB|=c=20 z tw. Pitagorasa
∡FAF≡∡ABC
| 12 | ||
W ΔABC: sinβ= | ||
| 20 |
| x | ||
WΔEFA: sin β= | ||
| 12 |
| x | 12 | |||
⇔ | = | ⇔x=7.2 | ||
| 12 | 20 |
 Otwórz linka ,który podał kemw
Tam ma inne dane a tu innne .......... ( i co mamy o tym myśleć?
Otwórz linka ,który podał kemw
Tam ma inne dane a tu innne .......... ( i co mamy o tym myśleć?
 miło.
Może są dwie wersje?
Zobacz zadanie "seksinstruktora".
miło.
Może są dwie wersje?
Zobacz zadanie "seksinstruktora".