| tgα | ||
sinα= | ||
| √1+tg2α |
| 1 | ||
cosα= | ||
| √1+tg2α |
| sinx | √5 | √5 | ||||
tgx= | = | to sinx= | cosx | |||
| cosx | 2 | 2 |
| 5 | ||
sin2x= | cos2x | |
| 4 |
| 5 | ||
1−cos2x= | cos2x | |
| 4 |
| 9 | 4 | 2 | 2 | |||||
1= | cos2x ⇒cos2x= | to cosx= | lub cosx= − | |||||
| 4 | 9 | 3 | 3 |
| 4 | 5 | √5 | √5 | |||||
sinx2x= 1−cos2x= 1− | = | to sinx= | lub sinx= − | |||||
| 9 | 9 | 3 | 3 |
a mam jeszcze jedno
zadanie.
wiedząc, że sinαcosα= 13 oblicz w= ( tgα + 1tgα ) 2
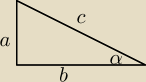1) tego typu najprościej podstawiamy a=√5 b =2 c= z Pitagorasa
| sinα | ||
2)tgα= | wspólny mianownik ... | |
| cosα |